
分析 求出集合P的等价条件,根据充分条件和必要条件的定义建立方程关系进行求解即可.
解答 解:P={x|x2-8x-20≤0}={x|-2≤x≤10},
若存在实数m,使x∈P是x∈S的充要条件,
则$\left\{\begin{array}{l}{1+m≥1-m}\\{1+m=10}\\{1-m=-2}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥0}\\{m=9}\\{m=3}\end{array}\right.$,此时m无解,
即不存在实数m,使x∈P是x∈S的充要条件.
点评 本题主要考查充分条件和必要条件的应用,求出集合的等价条件,建立不等式关系是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
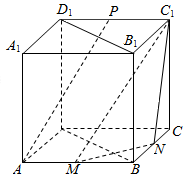 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1)
如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]∪[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]和[$\frac{2π}{3}$,π] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com