
【题目】已知直线![]() :
:![]() 和圆
和圆![]() :
:![]() .
.
(1)求证:直线![]() 恒过一定点
恒过一定点![]() ;
;
(2)试求当![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 所截得的弦长最短;
所截得的弦长最短;
(3)在(2)的前提下,直线![]() 是过点
是过点![]() ,且与直线
,且与直线![]() 平行的直线,求圆心在直线
平行的直线,求圆心在直线![]() 上,且与圆
上,且与圆![]() 相外切的动圆中半径最小圆的标准方程.
相外切的动圆中半径最小圆的标准方程.
【答案】(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)通过直线l转化为直线系,求出直线恒过的定点;
(2)当直线![]() 与
与![]() 垂直时,所截得的弦长最短,此时有
垂直时,所截得的弦长最短,此时有![]()
![]() =-1,由此能出m的值;
=-1,由此能出m的值;
(3)由(2)得直线![]() 的方程为
的方程为![]() ,可判断出直线
,可判断出直线![]() 与圆
与圆![]() 相离,设动圆圆心为
相离,设动圆圆心为![]() ,当圆心
,当圆心![]() 到圆心
到圆心![]() 的距离最小时,动圆
的距离最小时,动圆![]() 的半径最小,从而得到最小圆的标准方程.
的半径最小,从而得到最小圆的标准方程.
(1)证明:直线![]() 的方程可化为:
的方程可化为:![]() .
.
解方程组![]() ,得
,得![]() .
.
所以,直线![]() 恒过定点
恒过定点![]() .
.
(2)解:圆![]() :
:![]() 的标准方程为
的标准方程为![]() ,
,
表示以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,
![]() ,
,![]() ,
,
∴![]() 在圆
在圆![]() 内,那么对任意
内,那么对任意![]() 都有直线
都有直线![]() 与圆
与圆![]() 相交.
相交.
当直线![]() 与
与![]() 垂直时,所截弦长最短.
垂直时,所截弦长最短.
又直线![]() 的斜率
的斜率![]() ,∴此时直线
,∴此时直线![]() 的斜率为
的斜率为![]() .
.
即![]() ,解得
,解得![]() .
.
(3)解:由(2)得直线![]() 的斜率为
的斜率为![]() ,又∵
,又∵![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
又圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,所以直线
,所以直线![]() 与圆
与圆![]() 相离.
相离.
设动圆圆心为![]() ,当圆心
,当圆心![]() 到圆心
到圆心![]() 的距离最小时,动圆
的距离最小时,动圆![]() 的半径最小,
的半径最小,
此时圆心![]() 为过点
为过点![]() 且与
且与![]() 垂直的直线与
垂直的直线与![]() 的交点,且动圆半径的最小值为
的交点,且动圆半径的最小值为![]() .
.
又过点![]() 与
与![]() 垂直的直线方程为
垂直的直线方程为![]() ,即
,即![]() .
.
解方程组![]() ,得
,得![]() .
.
即圆心![]() 为
为![]() .
.
∴所求圆的标准方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》里面提出“新建住宅要推广街区制,原则上不再建设封闭住宅小区,已建成的封闭小区和单位大院要逐步打开”,这个消息在网上一石激起千层浪,各种说法不一而足.某网站为了解居民对“开放小区”认同与否,从![]() 岁的人群中随机抽取了
岁的人群中随机抽取了![]() 人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对
人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对![]() 人对这“开放小区”认同情况进行统计得到下表:
人对这“开放小区”认同情况进行统计得到下表:
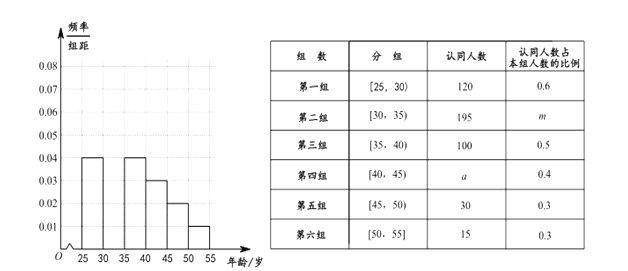
(Ⅰ)完成所给的频率分布直方图,并求![]() 的值;
的值;
(Ⅱ)如果从![]() 两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在
两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在![]() 内的概率 .
内的概率 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的奇数项成等差数列,偶数项成等比数列,且公差和公比都是2,若对满足m+n≤5的任意正整数m,n,均有am+an=am+n成立. (I)求数列{an}的通项公式;
(II)若bn=  ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间[x1 , x2]长度为x2﹣x1(x2>x1),已知函数f(x)= ![]() (a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值是 .
(a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点. (Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为θ,求sinθ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (b∈R).若存在x∈[
(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,则实数 b的取值范围是( )
,2],使得f(x)+xf′(x)>0,则实数 b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣∞,3)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一数学研究小组测量学校的一座教学楼AB的高度![]() 已知测角仪器距离地面的高度为h米,现有两种测量方法:
已知测角仪器距离地面的高度为h米,现有两种测量方法:
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A,计算并记录仰角
用测角仪器,对准教学楼的顶部A,计算并记录仰角![]() ;
;![]() 后退a米,重复
后退a米,重复![]() 中的操作,计算并记录仰角
中的操作,计算并记录仰角![]() .
.
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角
用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角![]() ,测试点与教学楼的水平距离b米.
,测试点与教学楼的水平距离b米.
请你回答下列问题:
![]() 用数据
用数据![]() ,
,![]() ,a,h表示出教学楼AB的高度;
,a,h表示出教学楼AB的高度;
![]() 按照方法II,用数据
按照方法II,用数据![]() ,b,h表示出教学楼AB的高度.
,b,h表示出教学楼AB的高度.
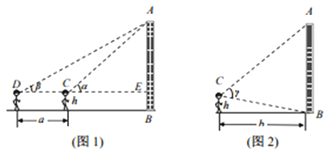
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com