
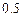 ,
,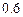 ,
,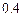 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为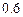 ,
,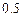 ,
,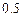 。
。 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:不详 题型:单选题
A. | B.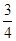 | C.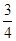 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为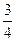 ,
,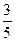 .
.
 的数学期望;
的数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,现就某事可行与否征求各顾问的意见,并按顾问中多数人的意见作出决策,那么作出正确的决策的概率 ..
,现就某事可行与否征求各顾问的意见,并按顾问中多数人的意见作出决策,那么作出正确的决策的概率 ..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中有
中有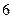 张卡片,其中
张卡片,其中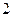 张写有数字
张写有数字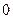 ,
,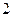 张写有数字
张写有数字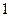 ,
,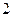 张写有数字
张写有数字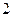 ;乙箱中也有
;乙箱中也有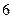 张卡片,其中
张卡片,其中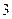 张写有数
张写有数 字
字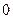 ,
,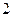 张写有数字
张写有数字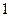 ,
,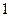 张写有数字
张写有数字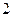 .
.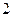 张卡片上数字之积为
张卡片上数字之积为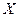 ,求
,求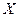 的
的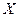 的
的 数学期望;
数学期望;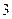 张卡片都写有
张卡片都写有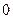 的概率是多少?
的概率是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 性别 专 业 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
 列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。
列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
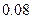 ,只选修甲和乙的概率是
,只选修甲和乙的概率是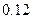 ,至少选修一门的概率是
,至少选修一门的概率是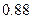 ,用
,用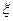 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.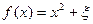
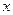 为
为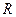 上的偶函数”为事件
上的偶函数”为事件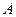 ,求事件
,求事件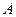 的概率;
的概率;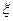 的分布列和数学期望。
的分布列和数学期望。 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com