
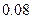 ,只选修甲和乙的概率是
,只选修甲和乙的概率是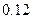 ,至少选修一门的概率是
,至少选修一门的概率是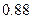 ,用
,用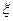 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.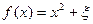
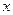 为
为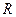 上的偶函数”为事件
上的偶函数”为事件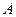 ,求事件
,求事件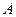 的概率;
的概率;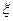 的分布列和数学期望。
的分布列和数学期望。  名题金卷系列答案
名题金卷系列答案科目:高中数学 来源:不详 题型:解答题
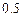 ,
,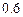 ,
,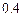 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为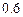 ,
,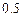 ,
,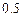 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
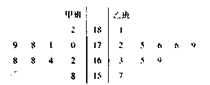
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
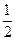 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: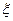 的分布列与期望E
的分布列与期望E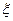 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
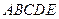 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.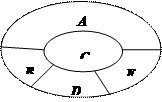
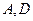 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数; 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率;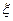 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量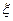 的分布列及其数学期望
的分布列及其数学期望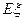 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
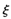 的分布列与数学期望.
的分布列与数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
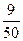 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com