
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 “试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做
“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做 了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为
了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为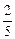 。
。 的人数
的人数 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 性别 专 业 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
 列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。
列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
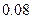 ,只选修甲和乙的概率是
,只选修甲和乙的概率是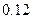 ,至少选修一门的概率是
,至少选修一门的概率是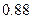 ,用
,用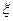 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.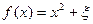
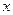 为
为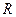 上的偶函数”为事件
上的偶函数”为事件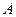 ,求事件
,求事件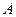 的概率;
的概率;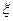 的分布列和数学期望。
的分布列和数学期望。 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 小题满分12分)
小题满分12分)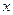 ,“实用性”得分为
,“实用性”得分为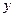 ,统计结果如下表:
,统计结果如下表: 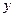 作品数量 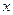 | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
| 创 新 性 | 1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | 1 | 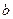 | 6 | 0 | 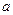 | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
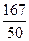 ,求
,求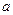 、
、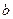 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
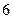 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为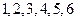 .
.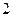 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有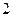 次抽到
次抽到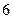 号球的概率;
号球的概率; 个球,记球的最大编号为
个球,记球的最大编号为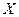 ,求随机变量
,求随机变量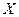 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,甲胜丙的概
,甲胜丙的概 ,乙胜丙的概率为
,乙胜丙的概率为 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与 未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束
未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
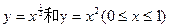 的图象围成的图形.
的图象围成的图形.A. | B. | C.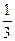 | D.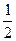 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

 内的频率为
内的频率为| A.0.15 | B.0.08 | C.0.23 | D.0.67 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com