
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(3)求证:当![]() 时,
时,![]() .
.
【答案】(1)见解析;(2)2;(3)见证明
【解析】
(1)求出原函数的导函数f′(x)![]() (x>0),讨论a≥0,和a<0,由f′(x)的正负确定函数的单调性;
(x>0),讨论a≥0,和a<0,由f′(x)的正负确定函数的单调性;
(2)a≤0,不满足f(x)≤0恒成立. a>0,由(1)求得函数的最大值,构造函数结合零点存在定理求其最值的范围,求得![]() 的最小值
的最小值
(3)由(2)可知f(x)=lnx﹣2x2+1<0,得到ex﹣xlnx+2x3﹣x2+x﹣1>ex﹣x2+2x﹣1.
构造u(x)=ex﹣x2+2x﹣1(x>0),利用两次求导证明ex﹣xlnx+2x3﹣x2+x﹣1>0.
(1)解:f(x)=lnx-ax2+(-a+2)x+1,f′(x)![]() 2ax-a+2
2ax-a+2![]() (x>0),
(x>0),
①若a≤0,则f′(x)>0,函数f(x)在(0,+∞)上单调递增;
②若a>0,由f′(x)>0,得0<x![]() ;由f′(x)<0,得x
;由f′(x)<0,得x![]() .
.
∴函数f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减;
,+∞)上单调递减;
(2)若a≤0,则f(1)=-2a+3>0,∴不满足f(x)≤0恒成立.
若a>0,由(1)可知,函数f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
∴![]() ,又f(x)≤0恒成立,
,又f(x)≤0恒成立,
∴![]() 0,
0,
设g(x)=lnx+x,则g(![]() )≤0.
)≤0.
∵函数g(x)在(0,+∞)上单调递增,且g(1)=1>0,g(![]() )
)![]() 0,
0,
∴存在唯一的x0∈(![]() ),使得g(x0)=0.
),使得g(x0)=0.
当x∈(0,x0)时,g(x)<0,当x∈(x0,+∞)时,g(x)>0.
∴0![]() x0,解得a≥
x0,解得a≥![]() ∈(1,2),
∈(1,2),
又a∈Z,∴a≥2.
则综上a的最小值为2;
(3)由(2)可知,a=2时,f(x)=lnx﹣2x2+1<0,
∴lnx<2x2﹣1,则﹣xlnx>﹣2x3+x,
∴ex﹣xlnx+2x3﹣x2+x﹣1>ex﹣2x3+x+2x3﹣x2+x﹣1=ex﹣x2+2x﹣1.
记u(x)=ex﹣x2+2x﹣1(x>0),则u′(x)=ex﹣2x+2.
记h(x)=ex﹣2x+2,则h′(x)=ex﹣2,
由h′(x)=0,得x=ln2.
当x∈(0,ln2)时,h′(x)<0,当x∈(ln2,+∞)时,h′(x)>0,
∴函数h(x)在(0,ln2)上单调递减,在(ln2,+∞)上单调递增,
![]() .
.
∴h(x)>0,即u′(x)>0,故函数u(x)在(0,+∞)上单调递增.
∴u(x)>u(0)=e0﹣1=0,即ex﹣x2+2x﹣1>0.
∴ex﹣xlnx+2x3﹣x2+x﹣1>0.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为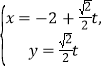 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:

(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5张奖券中有2张是中奖的,先由甲抽1张,然后由乙抽1张,抽后不放回,求:
(1)甲中奖的概率![]() ;
;
(2)甲、乙都中奖的概率![]() ;
;
(3)只有乙中奖的概率![]() ;
;
(4)乙中奖的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若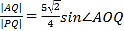 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏公司对今年新开发的一些游戏进行评测,为了了解玩家对游戏的体验感,研究人员随机调查了300名玩家,对他们的游戏体验感进行测评,并将所得数据统计如图所示,其中![]() .
.

(1)求这300名玩家测评分数的平均数;
(2)由于该公司近年来生产的游戏体验感较差,公司计划聘请3位游戏专家对游戏进行初测,如果3人中有2人或3人认为游戏需要改进,则公司将回收该款游戏进行改进;若3人中仅1人认为游戏需要改进,则公司将另外聘请2位专家二测,二测时,2人中至少有1人认为游戏需要改进的话,公司则将对该款游戏进行回收改进.已知该公司每款游戏被每位专家认为需要改进的概率为![]() ,且每款游戏之间改进与否相互独立.
,且每款游戏之间改进与否相互独立.
(i)对该公司的任意一款游戏进行检测,求该款游戏需要改进的概率;
(ii)每款游戏聘请专家测试的费用均为300元/人,今年所有游戏的研发总费用为50万元,现对该公司今年研发的600款游戏都进行检测,假设公司的预算为110万元,判断这600款游戏所需的最高费用是否超过预算,并通过计算说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若对任意正整数![]() ,不等式
,不等式![]() 均成立,求
均成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,焦距为2c,圆
,焦距为2c,圆![]() ,
,![]() ,
,![]() 是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形
是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形![]() 面积的最大值为
面积的最大值为![]() .
.

(1)求椭圆C的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于M,N两点,直线
与圆O相切,且与椭圆相交于M,N两点,直线![]() 与
与![]() 平行且与椭圆相切于P(O,P两点位于
平行且与椭圆相切于P(O,P两点位于![]() 的同侧),求直线
的同侧),求直线![]() ,
,![]() 距离d的取值范围.
距离d的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com