
分析 由分母不为零求出sinx-cosx≠-1,再设t=sinx-cosx,利用两角和的正弦公式化简,求出t的范围,由平方关系表示出sinxcosx,代入解析式化简,再由t的范围和一次函数的单调性,求出原函数的值域.
解答 解:函数y=$\frac{sinxcosx}{1+sinx-cosx}$,
∵分母不能为零,即sinx-cosx≠-1,
设t=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),
∴$-\sqrt{2}≤t≤\sqrt{2}$,且t≠-1.
则sinx•cosx=$\frac{{t}^{2}-1}{2}$,
可得函数y=$\frac{sinxcosx}{1+sinx-cosx}$=$\frac{\frac{{t}^{2}-1}{2}}{1+t}$=$\frac{1}{2}$(t-1)=$\frac{1}{2}t-\frac{1}{2}$
根据一次函数的单调性,可得函数y的值域为[$-\frac{\sqrt{2}+1}{2}$,-1)∪(-1,$\frac{\sqrt{2}-1}{2}$].
故答案为:[$-\frac{\sqrt{2}+1}{2}$,-1)∪(-1,$\frac{\sqrt{2}-1}{2}$].
点评 本题主要考查了“sinx-cosx”和“sinxcosx”的关系,利用平方关系建立关系式,以及换元法求函数的最值问题,注意换元后需要求出未知数的范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
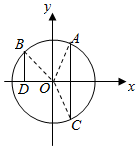 (理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.
(理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2}{3},1)$ | B. | $[\frac{1}{3},1)$ | C. | $[\frac{1}{3},1)∪(1,3]$ | D. | (1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com