考点:直线与平面垂直的性质,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)首先,得到BD⊥AC,然后,得到A1O⊥BD,最后,得到BD⊥面A1AC即可;
(2)首先,得到A1B1∥AB AB∥CD,然后,得到四边形A1B1CD是平行四边形,从而得到证明结论;
(3)直接根据体积公式进行求解即可.
解答:
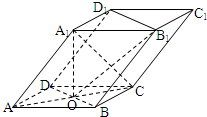
解:(1)证明:∵底面ABCD是正方形,
∴BD⊥AC,
又∵A
1O⊥平面ABCD且BD?面ABCD,
∴A
1O⊥BD,
又∵A
1O∩AC=O,A
1O?面A
1AC,AC?面A
1AC,
∴BD⊥面A
1AC,AA
1?面A
1AC,
∴AA
1⊥BD.
(2)∵A
1B
1∥AB,AB∥CD,
∴A
1B
1∥CD,
又A
1B
1=CD,
∴四边形A
1B
1CD是平行四边形,
∴A
1D∥B
1C,同理A
1B∥CD
1,
∵A
1B?平面A
1BD,A
1D?平面A
1BD,CD
1?平面CD
1B
1,B
1C?平面CD
1B,
且A
1B∩A
1D=A
1,CD
1∩B
1C=C,
∴平面A
1BD∥平面CD
1B
1.
(3)∵A
1O⊥面ABCD,
∴A
1O是三棱柱A
1B
1D
1-ABD的高,
在正方形ABCD中,AO=1.
在Rt△A
1OA中,AA
1=2,AO=1,
∴A
1O=
,
∴V
三棱柱ABD-A1B1D1=S
△ABD•A
1O=
•(
)
2•
=
∴三棱柱ABD-A
1B
1D
1的体积为
.
点评:本题考查了空间中点线面的位置关系,例如直线与平面平行、垂直,平面和平面平行等知识,属于中档题.

 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=


 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1.