
分析 由题意知方程的判别式大于等于零求出m的范围,再判断出所求的事件符合几何概型,再由几何概型的概率公式求出所求事件的概率.
解答 解:若关于x的方程x2+2mx+m+2=0有实根,则△=(2m)2-4×(m+2)≥0,
即m2-m-2≥0,解得m≥2或m≤-1;
记事件A:设在区间[0,6]上随机地取一个数m,方程x2+2mx+m+2=0有实根符合几何概型,
∴P(A)=$\frac{6-2}{6-0}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了求几何概型下的随机事件的概率,即求出所有实验结果构成区域的长度和所求事件构成区域的长度,再求比值.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 四棱锥四个侧面中不存在两组侧面互相垂直 | |
| B. | 四棱锥的四个侧面可能全是直角三角形 | |
| C. | 若该四棱锥的左视图为直角三角形,则体积为$\frac{4}{3}$ | |
| D. | 若该四棱锥的正视图为等腰三角形,则四棱锥的侧面积为6+2$\sqrt{2}$+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
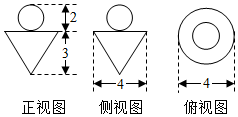
| A. | 5π | B. | $\frac{40π}{3}$ | C. | $\frac{20π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+x}{1-x}$ | B. | $\frac{x-1}{x+1}$ | C. | x | D. | -$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -$\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | -$\frac{24}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1+2$\sqrt{2}$,+∞) | B. | (-∞,1-2$\sqrt{2}$] | C. | [1-2$\sqrt{2}$,0] | D. | [-2,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com