
分析 根据向量数量积的定义结合三角形的面积公式,以及余弦定理消去cosA,结合基本不等式的应用进行求解即可.
解答 解:设A、B、C所对边分别为a,b,c,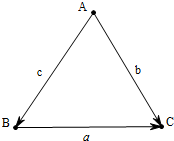
由$\overrightarrow{AB}$•$\overrightarrow{AC}$=2,得bccosA=5 ①,
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bc$\sqrt{1-co{s}^{2}A}$=$\frac{1}{2}$bc$\sqrt{1-\frac{25}{{b}^{2}{c}^{2}}}$=$\frac{1}{2}$$\sqrt{{b}^{2}{c}^{2}-25}$
由余弦定理可得b2+c2-2bccosA=16②,
由①②消掉cosA得b2+c2=26,所以b2+c2≥2bc,bc≤13,当且仅当b=c=$\sqrt{13}$时取等号,
所以S△ABC=$\frac{1}{2}$$\sqrt{{b}^{2}{c}^{2}-25}$≤$\frac{1}{2}$$\sqrt{1{3}^{2}-25}$=6,
故△ABC的面积的最大值为6,
故答案为:6.
点评 本题考查平面向量数量积的运算、三角形面积公式不等式求最值等知识,综合性较强,有一定难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P=Q | B. | P⊆Q | C. | P?Q | D. | P∩Q=ϕ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
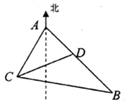 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com