
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
分析 设$\vec a$-$\vec b$与$\vec b$的夹角为θ,由题意求得$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,1),再根据cosθ=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{b}|}$ 的值,求得θ的值.
解答 解:设$\vec a$-$\vec b$与$\vec b$的夹角为θ,∵向量$\vec a$=(-l,2),$\vec b$=(2,1),∴$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,1),
cosθ=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{b}|}$=$\frac{-6+1}{\sqrt{10}•\sqrt{5}}$=-$\frac{\sqrt{2}}{2}$,∴θ=135°,
故选:D.
点评 本题主要考查两个向量的数量积公式,两个向量坐标形式的运算法则,属于基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
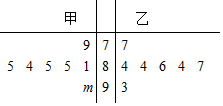 如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )
如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 1 | 2 | 4 | 5 |
| 销售额y(万元) | 6 | 14 | 28 | 32 |
| A. | 66.2万元 | B. | 66.4万元 | C. | 66.8万元 | D. | 67.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 △ABC的三边a,b,c所对的角分别为A,B,C,已知bcosC=ccosB.
△ABC的三边a,b,c所对的角分别为A,B,C,已知bcosC=ccosB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com