
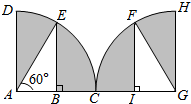
 如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)
如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14) 分析 由已行求出GH=5$\sqrt{2}$,AB=5,BE=5$\sqrt{3}$,GI=$\frac{5\sqrt{2}}{2}$,FI=$\frac{5\sqrt{6}}{2}$,由此利用两个四分之一圆面积之和减去两个直角三角形面积之和,能求出阴影部分面积.
解答 解:∵两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,
∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,
∴GH=$\sqrt{\frac{100}{2}}$=5$\sqrt{2}$,AB=10cos60°=5,BE=10×sin60°=5$\sqrt{3}$,
GI=5$\sqrt{2}cos60°$=$\frac{5\sqrt{2}}{2}$,FI=5$\sqrt{2}$sin60°=$\frac{5\sqrt{6}}{2}$,
∴S阴=$\frac{1}{4}π[1{0}^{2}+(5\sqrt{2})^{2}]$-$\frac{1}{2}×5×5\sqrt{3}-\frac{1}{2}×\frac{5\sqrt{2}}{2}×\frac{5\sqrt{6}}{2}$≈85.28.
故答案为:85.28.
点评 本题考查阴影部分面积的求法,是基础题,解题时要认真审题,注意圆的面积公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-3=0 | B. | x-2y+3=0 | C. | 2x-y+3=0 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-1,0] | C. | [1,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(x-$\frac{π}{6}$) | C. | y=sinx+$\frac{π}{6}$ | D. | y=sinx-$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com