
设数列{an}满足an+1 = 2an + n2 - 4n + 1.
(1)若a1 = 3,求证:存在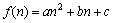 (a,b,c为常数),
(a,b,c为常数), 使数列{ an + f(n) }是等比数列,并求出数列{an}的通项公式;
使数列{ an + f(n) }是等比数列,并求出数列{an}的通项公式;
(2)若an 是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com