
分析 (1)根据平面向量的数量积公式和三角恒等变换化简f(x),根据正弦函数的性质求出f(x)的零点;
(2)根据f(A)=1求出A,利用正弦定理和正弦函数的性质得出$\frac{b+c}{a}$的范围.
解答 解:(1)由条件可知:$\overrightarrow a•\overrightarrow b=cosx•sin(x-\frac{π}{6})+sinx•cos(x-\frac{π}{6})=sin(2x-\frac{π}{6})$,
∴$f(x)=\overrightarrow a•\overrightarrow b=sin(2x-\frac{π}{6})$.
令$sin(2x-\frac{π}{6})=0$,得2x-$\frac{π}{6}$=kπ,∴$x=\frac{kπ}{2}+\frac{π}{12}$,k∈Z.
∴f(x)的零点为$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
(2)由正弦定理得$\frac{b+c}{a}=\frac{sinB+sinC}{sinA}$
由(1)f(A)=sin(2A-$\frac{π}{6}$)=1,
∴$2A-\frac{π}{6}=2kπ+\frac{π}{2}$,k∈Z,又A∈(0,π),∴$A=\frac{π}{3}$,
∴$C=\frac{2π}{3}-B$,
∴$\frac{b+c}{a}=\frac{{sinB+sin(\frac{2π}{3}-B)}}{sinA}=\frac{{\frac{3}{2}sinB+\frac{{\sqrt{3}}}{2}cosB}}{sinA}=\frac{{\sqrt{3}sin(B+\frac{π}{6})}}{sinA}=2sin(B+\frac{π}{6})$,
∵$0<B<\frac{2π}{3}$,∴$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,∴$\frac{1}{2}<sin(B+\frac{π}{6})≤1$.
∴$1<\frac{b+c}{a}≤2$.
点评 本题考查了平面向量的数量积运算,三角恒等变换,正弦定理,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
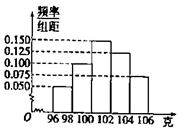 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A. | 90 | B. | 75 | C. | 60 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
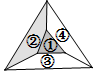 《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写的信中提到:“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”回答他这个问题用了124年,但简单的图形我们能用逐一列举的方法解决.若用红、黄、蓝、绿四种颜色给右边的地图着色,假定区域①已着红色,区域②已着黄色,则剩余的区域③④共有2种着色方法.
《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写的信中提到:“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”回答他这个问题用了124年,但简单的图形我们能用逐一列举的方法解决.若用红、黄、蓝、绿四种颜色给右边的地图着色,假定区域①已着红色,区域②已着黄色,则剩余的区域③④共有2种着色方法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com