
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
分析 由已知可得函数f(x)是周期为2的周期函数,作出函数f(x)与g(x)的图象,数形结合得答案.
解答 解:函数h(x)=f(x)-g(x)的零点,
即方程函数f(x)-g(x)=0的根,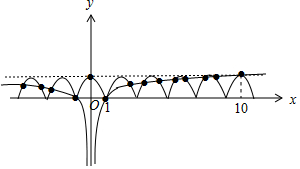
也就是两个函数y=f(x)
与y=g(x)图象交点的横坐标,
由f(x+2)=f(x),
可得f(x)是周期为2的周期函数,
又g(x)=$\left\{\begin{array}{l}{lg|x|,x≠0}\\{1,x=0}\end{array}\right.$,
作出两函数的图象如图:
∴函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为14.
故选:D.
点评 本题考查函数零点的判定定理,考查数学转化思想方法与数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,-$\frac{7}{2}$) | B. | ($\frac{5}{2}$,$\frac{7}{2}$) | C. | ($\frac{3}{2}$,-$\frac{7}{2}$) | D. | ($\frac{3}{2}$,$\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
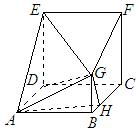 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 未感冒 | 感冒 | 合计 | |
| 用某种药 | 252 | 248 | 500 |
| 未用某种药 | 224 | 276 | 500 |
| 合计 | 476 | 524 | 1000 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com