
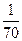 、
、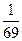 、
、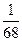 ,且各道工序互不影响,则加工出来的零件的次品率为____________ .
,且各道工序互不影响,则加工出来的零件的次品率为____________ . 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
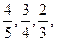 且每个问题回答正确与否相互独立。
且每个问题回答正确与否相互独立。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
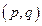 ,在
,在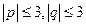 中按均匀分布出现.
中按均匀分布出现.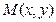 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点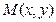 落在上述区域的概率?
落在上述区域的概率?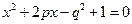 有两个实数根的概率.
有两个实数根的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
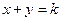 (
(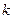 为常数)上且使此事件的概率最大,求
为常数)上且使此事件的概率最大,求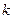 的值;
的值;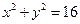 内部的概率.
内部的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 跳格游戏:如右图,人从格外只能进入第1格,在格中每次可向前跳1格或2格,那么人从格外跳到第8格的方法种数为( )
跳格游戏:如右图,人从格外只能进入第1格,在格中每次可向前跳1格或2格,那么人从格外跳到第8格的方法种数为( )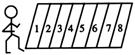
| A.8种 | B.13种 |
| C.21种 | D.34种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
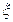 ~
~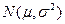 ,且
,且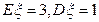 ,那么
,那么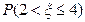 等于( )
等于( )| A.0.5 | B.0.683 | C.0.954 | D.0.997 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com