
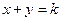 (
(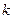 为常数)上且使此事件的概率最大,求
为常数)上且使此事件的概率最大,求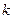 的值;
的值;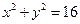 内部的概率.
内部的概率. 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:不详 题型:填空题
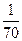 、
、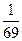 、
、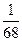 ,且各道工序互不影响,则加工出来的零件的次品率为____________ .
,且各道工序互不影响,则加工出来的零件的次品率为____________ .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
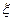 为本场比赛的局数.求
为本场比赛的局数.求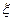 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
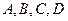 四个问题,规则如下:
四个问题,规则如下: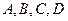 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;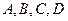 顺序作答,直至答题结束.
顺序作答,直至答题结束.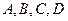 回答正确的概率依次为
回答正确的概率依次为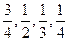 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.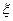 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求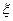 的分布列和数学的
的分布列和数学的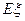 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
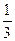 ,甲胜丙的概率为
,甲胜丙的概率为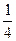 ,乙胜丙的概率为
,乙胜丙的概率为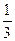 ;
;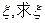 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
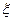 为甲得的分数,求随机变量
为甲得的分数,求随机变量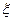 的概率分布列和数学期望.
的概率分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:
面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:| 落在桌面的数字 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 32 | 18 | 15 | 13 | 22 |
| A.0.22 | B.0.35 | C.0.65 | D.0.78 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
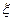 表示摸出的黑球数,写出
表示摸出的黑球数,写出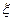 的分布列并求
的分布列并求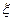 的数学期望.
的数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com