
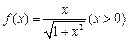 ,数列
,数列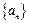 满足
满足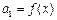 ,
,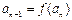 .
.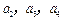 ;
;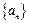 的通项,并予以证明.
的通项,并予以证明. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, ,求证
,求证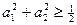 .
. ,
,
 ,恒有
,恒有 ≥0,所以
≥0,所以 ≤0,从而得
≤0,从而得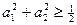 ,
, ,
, ,请写出上述结论的推广式;
,请写出上述结论的推广式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
.类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,然后它接着按图示在
,然后它接着按图示在 轴、
轴、 轴的平行方向向右、向上来回运动,且每秒移动一个单位长度,求
轴的平行方向向右、向上来回运动,且每秒移动一个单位长度,求 秒时,这个粒子所处的位置
秒时,这个粒子所处的位置
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
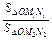 =
=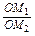 ·
·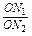 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.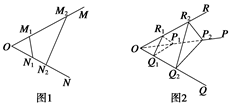
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
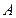 、
、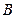 两点,则当
两点,则当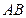 与抛物线的对称轴垂直时,
与抛物线的对称轴垂直时,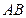 的长度最短;试将上述命题类比到其他曲线,写出相应的一个真命题为 .
的长度最短;试将上述命题类比到其他曲线,写出相应的一个真命题为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.矩形都是四边形; | B.四边形的对角线都相等; |
| C.矩形都是对角线相等的四边形; | D.对角线都相等的四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com