
分析 (1)根据向量的坐标运算和向量的夹角公式即可求出,
(2)根据向量的平行的条件得到-5k=5×2,解得即可,
(3)根据向量的垂直的条件得到-5×5+5k=0,解得即可.
解答 解:(1)设向量向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
∵$\overrightarrow{a}$=(3,0),$\overrightarrow{b}$=(-5,5),
∴$\overrightarrow{a}•\overrightarrow{b}$=3×(-5)+0×5=-15,|$\overrightarrow{a}$|=$\sqrt{{3}^{2}+{0}^{2}}$=3,|$\overrightarrow{b}$|=5$\sqrt{2}$
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-15}{3×5\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
又∵θ∈[0,π],
∴$θ=\frac{3}{4}π$
(2)∵$\overrightarrow{b}$∥$\overrightarrow{c}$,
∴-5k=5×2,
∴k=-2
(3)∵$\overrightarrow{a}+\overrightarrow{c}$=(5,k),
又$\overrightarrow{b}$⊥($\overrightarrow{a}+\overrightarrow{c}$),
∴$\overrightarrow{b}$•($\overrightarrow{a}+\overrightarrow{c}$)=0,
∴-5×5+5k=0,
∴k=5
点评 本题考查了向量的夹角公式和向量的垂直和平行的条件,属于基础题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
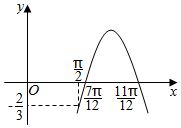 函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f($\frac{π}{2}$)=-$\frac{2}{3}$,则函数f(x)的表达式为( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f($\frac{π}{2}$)=-$\frac{2}{3}$,则函数f(x)的表达式为( )| A. | f(x)=$\frac{2}{3}$cos(3x-$\frac{π}{4}$) | B. | f(x)=$\frac{2}{3}$cos(3x+$\frac{π}{4}$) | C. | f(x)=$\frac{2}{3}$$\sqrt{2}$cos(3x+$\frac{π}{4}$) | D. | f(x)=$\frac{2}{3}$$\sqrt{2}$cos(3x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100π | B. | $\frac{256}{3}$π | C. | $\frac{100}{3}$π | D. | $\frac{500}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
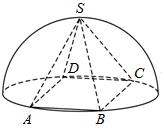 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该四棱锥的外接球的体积为( )
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该四棱锥的外接球的体积为( )| A. | $\frac{4\sqrt{2}}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{32\sqrt{2}}{3}$π | D. | $\frac{64\sqrt{2}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=7,b=14,A=30° | B. | a=20,b=26,A=150° | ||
| C. | a=30,b=40,A=30° | D. | a=72,b=60,A=135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com