
【题目】已知圆C的圆心坐标![]() 且与线y=3x+4相切,
且与线y=3x+4相切,
(1)求圆C的方程;
(2)设直线![]() 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
【答案】(1)(x-2)2+y2=10(2)y=-x+1+![]() 或y=-x+1-
或y=-x+1-![]()
【解析】
(1)由直线与圆相切得,圆心到直线的距离即为半径,从而得解;
(2)设M(x1,y1),N(x2,y2),进而通过直线与圆联立得到2x2-(4+2m)x+m2-6=0,由韦达定理可得MN中点H的坐标为(![]() ,
,![]() ),假设以MN为直径的圆经过原点,则有|OH|=
),假设以MN为直径的圆经过原点,则有|OH|=![]() |MN|,进而由垂径定理及坐标表示距离列方程求解即可.
|MN|,进而由垂径定理及坐标表示距离列方程求解即可.
(1)根据题意,![]()
所以圆的标准方程为:(x-2)2+y2=10;
(2)设M(x1,y1),N(x2,y2)是直线y=-x+m与圆C的交点,
联立y=-x+m与(x-2)2+y2=10可得:2x2-(4+2m)x+m2-6=0,
则有x1+x2=m+2,x1x2=![]() ,
,
则MN中点H的坐标为(![]() ,
,![]() ),
),
假设以MN为直径的圆经过原点,则有|OH|=![]() |MN|,
|MN|,
圆心C到MN的距离d=![]() ,
,
则有|MN|=2![]() =2
=2![]() ,
,
又由|OH|=![]() |MN|,
|MN|,
则有(![]() )2+(
)2+(![]() )2=10-
)2=10-![]() ,
,
解可得m=1±![]() ,
,
经检验,m=1±![]() 时,直线与圆相交,符合题意;
时,直线与圆相交,符合题意;
故直线MN的方程为:y=-x+1+![]() 或y=-x+1-
或y=-x+1-![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 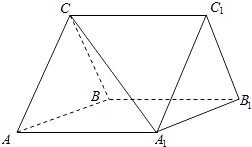
(1)证明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有穷数列![]() 中的每一项都是-1,0,1这三个数中的某一个数,
中的每一项都是-1,0,1这三个数中的某一个数,![]() ,且
,且![]()
![]()
![]() ,则有穷数列
,则有穷数列![]() 中值为0的项数是( )
中值为0的项数是( )
A. 1000B. 1010C. 1015D. 1030
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.

(1)如果![]() ,求乙组同学单位时间内引体向上次数的平均数和方差;
,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果![]() ,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com