
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】对于棱长为![]() 的正方体
的正方体![]() ,有如下结论,其中错误的是( )
,有如下结论,其中错误的是( )
A. 以正方体的顶点为顶点的几何体可以是每个面都为直角三角形的四面体;
B. 过点![]() 作平面
作平面![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,则
,则![]() 三点共线;
三点共线;
C. 过正方体中心的截面图形不可能是正六边形;
D. 三棱锥![]() 与正方体的体积之比为
与正方体的体积之比为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为 ![]() .
.
(1)求a,b;
(2)设过F2的直线l与C的左、右两支分别相交于A、B两点,且|AF1|=|BF1|,证明:|AF2|、|AB|、|BF2|成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图梯形ABCD中,AD∥BC,∠ABC=90°,AD∶BC∶AB=2∶3∶4,E,F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折,给出四个结论:①DF⊥BC;
②BD⊥FC;
③平面DBF⊥平面BFC;
④平面DCF⊥平面BFC.
则在翻折过程中,可能成立的结论的个数为( )
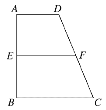
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)袋中装有黑色球和白色球共7个,从中任取2个球都是白色球的概率为![]() .现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
.现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
(1)求随机变量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M. 
(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心坐标![]() 且与线y=3x+4相切,
且与线y=3x+4相切,
(1)求圆C的方程;
(2)设直线![]() 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 三个警亭有直道相通,已知
三个警亭有直道相通,已知![]() 在
在![]() 的正北方向6千米处,
的正北方向6千米处,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处.
千米处.
(1)警员甲从![]() 出发,沿
出发,沿![]() 行至点
行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)警员甲从![]() 出发沿
出发沿![]() 前往
前往![]() ,警员乙从
,警员乙从![]() 出发沿
出发沿![]() 前往
前往![]() ,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达
,两人同时出发,甲的速度为3千米/小时,乙的速度为6千米/小时.两人通过专用对讲机保持联系,乙到达![]() 后原地等待,直到甲到达
后原地等待,直到甲到达![]() 时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?
时任务结束.若对讲机的有效通话距离不超过9千米,试问两人通过对讲机能保持联系的总时长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取![]() 人,从抽取的
人,从抽取的![]() 人中再随机地抽取
人中再随机地抽取![]() 人赠送小礼品,记这
人赠送小礼品,记这![]() 人中持“支持”态度的有
人中持“支持”态度的有![]() 人,求
人,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com