练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图梯形ABCD中，AD∥BC，∠ABC＝90°，AD∶BC∶AB＝2∶3∶4，E，F分别是AB，CD的中点,将四边形ADFE沿直线EF进行翻折，给出四个结论：①DF⊥BC；

    ②BD⊥FC；

    ③平面DBF⊥平面BFC；

    ④平面DCF⊥平面BFC.

    则在翻折过程中，可能成立的结论的个数为( )

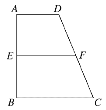
    A. 1 B. 2 C. 3 D. 4

    【答案】B

    【解析】分析：利用空间中线线、线面、面面间的位置关系求解.

    详解：

    对于①：因为BC∥AD，AD与DF相交不垂直，所以BC与DF不垂直,则①错误；

    对于②：设点D在平面BCF上的射影为点P,当BP⊥CF时就有BD⊥FC, 而AD:BC:AB＝2:3:4可使条件满足,所以②正确；

    对于③：当点P落在BF上时, DP平面BDF,从而平面BDF⊥平面BCF,所以③正确；

    对于④：因为点D的投影不可能在FC上，所以平面DCF⊥平面BFC不成立，即④错误．

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，过椭圆M： （a＞b＞0）右焦点的直线x+y﹣ =0交M于A，B两点，P为AB的中点，且OP的斜率为 ．
    （1）求M的方程
    （2）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等差数列{an}的前n项和为Sn ． 已知S3=a22 ， 且S1 ， S2 ， S4成等比数列，求{an}的通项式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数f（x）=sinx的图象向右平移 个单位后得到函数y=g（x）的图象，则函数y=f（x）+g（x）的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，满足，，数列满足，，且.

    （1）求数列的通项公式；

    （2）求证：数列是等差数列，求数列的通项公式；

    （3）若，数列的前项和为，对任意的，都有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(本题满分12分)已知一次函数f(x)满足：f(1)=2, f(2x)=2f(x)-1.

    (1) 求f(x)的解析式;

    (2) 设, 若|g(x)|－af(x)＋a≥0，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数的图像向左平移个单位长度，再将图像上所有点的横坐标伸长到原来的倍（纵坐标不变），得到的图像.

    （1）求的单调递增区间；

    （2）若对于任意的，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）从某校高一年级随机抽取名学生，获得了他们日平均睡眠时间（单位：小时）的数据，整理得到数据分组及频数分布表：

    组号

    分组

    频数

    频率

    （Ⅰ）求的值．

    （Ⅱ）若，补全表中数据，并绘制频率分布直方图．

    （Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，若上述数据的平均值为，求，的值，并由此估计该校高一学生的日平均睡眠时间不少于小时的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家庭记录了未使用节水龙头天的日用水量数据（单位：）和使用了节水龙头天的日用水量数据，得到频数分布表如下：

    未使用节水龙头天的日用水量频数分布表

    日用水量

    频数

    使用了节水龙头天的日用水量频数分布表

    日用水量

    频数

    （Ⅰ）作出使用了节水龙头天的日用水量数据的频率分布直方图；

    （Ⅱ）估计该家庭使用节水龙头后，一年能节省多少水？（一年按天计算，同一组中的数据以这组数据所在区间中点的值作代表）

    查看答案和解析>>

    同步练习册答案