
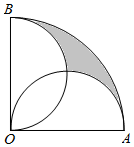 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,在扇形OAB内随机取一点,则此点取自阴影部分的概率是$\frac{1}{2}$-$\frac{1}{π}$.
如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,在扇形OAB内随机取一点,则此点取自阴影部分的概率是$\frac{1}{2}$-$\frac{1}{π}$. 分析 设OA=OB=2,两个半圆的交点为C,且以AO为直径的半圆以D为圆心,连结OC、CD.根据扇形面积公式和三角形面积公式算出S弓形OMC 算出两块阴影部分面积之和为π.最后根据几何概型计算公式,将所得阴影部分面积除以扇形OAB的面积,即可得到所求概率.
解答 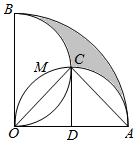 解:如图,设两个半圆的交点为C,且以AO为直径的半圆以D为圆心,连结OC、CD
解:如图,设两个半圆的交点为C,且以AO为直径的半圆以D为圆心,连结OC、CD
设OA=OB=2,则弓形OMC的面积为
S弓形OMC=S扇形OCD-SRt△DCO=$\frac{1}{4}$•π•12-$\frac{1}{2}$×1×1=$\frac{π}{4}$-$\frac{1}{2}$
可得空白部分面积为S空白=2S半圆AO-2S弓形OMC=2×$\frac{1}{2}$•π•12-($\frac{π}{2}$-1)=$\frac{π}{2}$+1,
因此,两块阴影部分面积之和S阴影=S扇形OAB-S空白=$\frac{1}{4}$π•22-($\frac{π}{2}$+1)=$\frac{π}{2}$-1
可得在扇形OAB内随机取一点,此点取自阴影部分的概率为P=$\frac{{S}_{阴影}}{{S}_{扇形AOB}}$=$\frac{\frac{π}{2}-1}{π}$=$\frac{1}{2}$-$\frac{1}{π}$,
故答案为:$\frac{1}{2}$-$\frac{1}{π}$
点评 本题主要考查几何概型的概率的计算,着重考查了扇形面积公式、组合图形的面积计算和几何概型计算公式等知识,根据条件求出阴影部分的面积是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 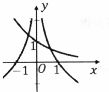 | B. | 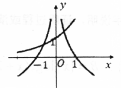 | C. | 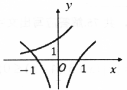 | D. | 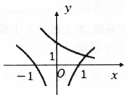 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com