练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．马路上有编号1，2，3，…，10共10盏灯，现要关掉其中的四盏，但不能关掉相邻的二盏或三盏，也不能关掉两端的两盏，则满足条件的关灯方案有20种．

    分析 先将亮的7盏灯排成一排，所以有6个符合条件的空位，即可得到结论．

    解答 解：因为关掉的三盏灯不是两端的灯，且任意两盏都不相邻，
    所以我使用插空法解决问题，即先将亮的7盏灯排成一排，
    因为两端的灯不能熄灭，
    所以有6个符合条件的空位，
    所以在6个空位中选取3个位置插入熄灭的3盏灯，即有C63=20种．
    故答案为：20

    点评 本题主要考查排列组合的应用，解决此类常用的方法是：特殊元素与特殊位置优先；相邻问题用捆绑的方法；不相邻问题用插空的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．已知cosα=$\frac{4}{5}$，α是第四象限角，则sin（2π-α）=（　　）
    A．$\frac{3}{5}$B．$\frac{4}{5}$C．±$\frac{3}{5}$D．-$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．从重量分别为1，2，3，4，…，10，11克的砝码（每种砝码各一个）中选出若干个，使其总重量恰为10克的方法总数为m，下列各式的展开式中x10的系数为m的选项是（　　）
    A．（1+x）（1+x2）（1+x3）…（1+x11）
    B．（1+x）（1+2x）（1+3x）…（1+11x）
    C．（1+x）（1+2x2）（1+3x3）…（1+11x11）
    D．（1+x）（1+x+x2）（1+x+x2+x3）…（1+x+x2+…+x11）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

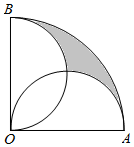    9．如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆，在扇形OAB内随机取一点，则此点取自阴影部分的概率是$\frac{1}{2}$-$\frac{1}{π}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知直线$\sqrt{3}$x+y-$\sqrt{3}$=0经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点和上顶点．
    （1）求椭圆C的标准方程；
    （2）过点（0，-2）的直线l与椭圆C交于不同的A，B两点，若∠AOB为钝角，求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．5名学生4名老师站成一排合影，5名学生站一起的排法种数为（　　）
    A．$A_5^5A_5^5$B．$A_4^4A_6^6$C．$A_4^4A_5^5$D．$A_5^5A_6^4$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在一次小型抽奖活动中，抽奖规则如下：一个不透明的口袋中共有6个大小相同的球，它们是1个红球，1个黄球，和4个白球，从中抽到红球中50元，抽到黄球中10元，抽到白球不中奖．某人从中一次性抽出两球，求：
    （1）该人中奖的概率；
    （2）该人获得的总奖金X（元）的分布列和均值E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

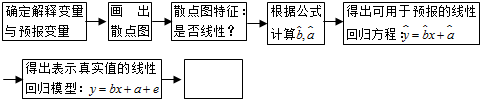
    10．小明为了更好地把握回归分析的知识，他试图用流程图形象地表示建立回归模型的过程：

    则最适合填写流程图中空白框的一项是（　　）
    A．预报B．计算真实值yC．比较模型效果D．残差异常分析

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．某生产基地有五台机器设备，现有五项工作待完成，每台机器完成每项工作获得的效益值如表所示．若每台机器只完成一项工作，且完成五项工作后获得的效益值总和最大，则下列描述正确的是②⑤ 
    ①甲只能承担第四项工作
    ②乙不能承担第二项工作
    ③丙可以不承担第三项工作
    ④丁可以承担第三项工作
    ⑤戊可以承担第四项工作
    请把描述正确说法的代号写到横线上．
    工作
    效益
    机器    		一二三四五
    甲1517141715
    乙2223212020
    丙913141210
    丁7911911
    戊1315141511

    查看答案和解析>>

    同步练习册答案