
分析 (1)由直线$\sqrt{3}$x+y-$\sqrt{3}$=0,分别令y=0,x=0,可得椭圆右焦点(1,0),上顶点(0,$\sqrt{3}$).又a=$\sqrt{{b}^{2}+{c}^{2}}$,即可得出.
(2)由题意可知:直线l的斜率垂直,可设直线l的方程为:y=kx-2.A(x1,y1),B(x2,y2).与椭圆方程联立化为(4k2+3)x2-16kx+4=0,△>0,可得k2$>\frac{1}{4}$.由∠AOB为钝角,∴$\overrightarrow{OA}•\overrightarrow{OB}$<0,利用数量积运算性质、根与系数的关系即可得出.
解答 解:(1)由直线$\sqrt{3}$x+y-$\sqrt{3}$=0,分别令y=0,x=0,可得椭圆右焦点(1,0),上顶点(0,$\sqrt{3}$).
∴c=1,b=$\sqrt{3}$,a=$\sqrt{{b}^{2}+{c}^{2}}$=2.
∴椭圆C的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)由题意可知:直线l的斜率垂直,可设直线l的方程为:y=kx-2.A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx-2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为(4k2+3)x2-16kx+4=0,
∵△>0,∴k2$>\frac{1}{4}$.
又x1+x2=$\frac{16k}{4{k}^{2}+3}$,x1x2=$\frac{4}{4{k}^{2}+3}$.
∵∠AOB为钝角,∴$\overrightarrow{OA}•\overrightarrow{OB}$<0,
∴x1x2+y1y2<0,x1x2+(kx1-2)(kx2-2)<0,化为:(1+k2)x1x2-2k(x1+x2)+4<0,
∴(1+k2)×$\frac{4}{4{k}^{2}+3}$-2k×$\frac{16k}{4{k}^{2}+3}$+4<0,化为k2$>\frac{4}{3}$.解得$k<-\frac{2\sqrt{3}}{3}$,或k$>\frac{2\sqrt{3}}{3}$,
∴直线l的斜率k的取值范围是$(-∞,\frac{-2\sqrt{3}}{3})$∪$(\frac{2\sqrt{3}}{3},+∞)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、向量数量积的运算性质、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 1 | C. | -$\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.
如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
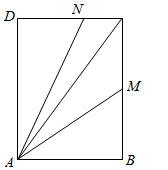 如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com