
 如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.
如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”. 分析 由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质.
解答 解:类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB”,可得三棱锥中截面的性质“如果面GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.
故答案为:GEF是中截面;截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$.
点评 本题主要考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想),属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢甜品 | 不喜欢甜品 | 总计 | |
| 广东游客 | 60 | 20 | 80 |
| 非广东游客 | 10 | 10 | 20 |
| 总计 | 70 | 30 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
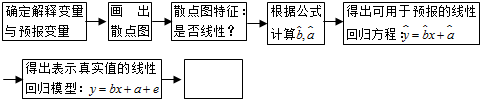
| A. | 预报 | B. | 计算真实值y | C. | 比较模型效果 | D. | 残差异常分析 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com