
| 喜欢甜品 | 不喜欢甜品 | 总计 | |
| 广东游客 | 60 | 20 | 80 |
| 非广东游客 | 10 | 10 | 20 |
| 总计 | 70 | 30 | 100 |
分析 (1)提出假设H0:广东游客和非广东游客在选用甜品的饮食习惯方面无差异,在H0下,求出K2=4.761>3.874,从而有95%的把握认为广东游客和非广东游客在选用甜品的饮食习惯方面有差异.
(2)不妨记5名珠海游客为A、B、C、D、E,其中A、B喜欢甜品,则从5名游客中随机抽取3人,利用列举法能求出至多有1人喜欢甜品的概率.
解答 解:(1)提出假设H0:广东游客和非广东游客在选用甜品的饮食习惯方面无差异,
在H0下,P(K2≥3.874)=0.05,
而K2=$\frac{100(600-200)^{2}}{70×30×20×80}$=4.761>3.874,
∴有95%的把握认为广东游客和非广东游客在选用甜品的饮食习惯方面有差异.
(2)不妨记5名珠海游客为A、B、C、D、E,其中A、B喜欢甜品,
则从5名游客中随机抽取3人,
基本事件为ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,
BDE,CDE,共10种情况,
至多有1人喜欢甜品的基本事件为ACD,ACE,ADE,
BCD,BCE,BDE,CDE,共7种情况,
故至多有1人喜欢甜品的概率$P=\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}+\sqrt{3}}{6}$ | B. | $\frac{2\sqrt{6}-1}{6}$ | C. | $\frac{2\sqrt{6}+1}{6}$ | D. | $\frac{2\sqrt{2}-\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.
如图,类比三角形中位线定理“如果EF是三角形的中位线,则EF$\underset{∥}{=}$$\frac{1}{2}$AB.”,在空间四面体(三棱锥)P-ABC中,“如果GEF是中截面,则截面GEF∥截面ABC且截面GEF1的面积等于于截面ABC的面积的$\frac{1}{4}$”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $3-2\sqrt{2}$ | D. | $3+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
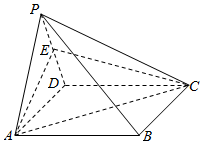 已知四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等边三角形,E为棱PD的中点
已知四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等边三角形,E为棱PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com