
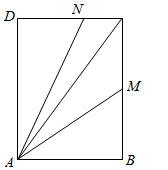
 如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$. 分析 【解法一】由题意建立平面直角坐标系,设点M(3,a),N(b,4),0<a<4,0<b<3;
求得b=$\frac{3-3x}{y}$,a=$\frac{4-4y}{x}$,从而可得$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=(x+y-1)2,
再设x+y=m,则x=m-y;利用判别式即可求出m的最小值;
【解法二】运用三角换元,根据方程组求出x,y;令$\frac{1}{4-a}$=sina,$\frac{1}{3-b}$=cosa,
计算x+y是一个关于sina,cosa的函数,比较容易看出它的最小值.
解答  解:【解法一】由题意建立平面直角坐标系,如图所示;
解:【解法一】由题意建立平面直角坐标系,如图所示;
设点M(3,a),N(b,4),且0<a<4,0<b<3;
∵$\overrightarrow{AC}$=(3,4),$\overrightarrow{AM}$=(3,a),$\overrightarrow{AN}$=(b,4);
又∵$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,(x+y≥1)
∴(3,4)=x(3,a)+y(b,4),
即$\left\{\begin{array}{l}{3x+yb=3}\\{xa+4y=4}\end{array}\right.$,
∴b=$\frac{3-3x}{y}$,a=$\frac{4-4y}{x}$,
∴$\frac{1}{{CM}^{2}}$+$\frac{1}{{CN}^{2}}$=$\frac{1}{{(4-a)}^{2}}$+$\frac{1}{{(3-b)}^{2}}$=$\frac{1}{16}$•$\frac{{x}^{2}}{{(x+y-1)}^{2}}$+$\frac{1}{9}$•$\frac{{y}^{2}}{{(x+y-1)}^{2}}$=1,
即$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=(x+y-1)2,
设x+y=m,则x=m-y;
则$\frac{{(m-y)}^{2}}{16}$+$\frac{{y}^{2}}{9}$=(m-1)2,
即25y2-18my+9m2-144(m-1)2=0,
故△=(18m)2-4×25×(9m2-144(m-1)2)≥0,
即24m2-50m+25≥0,
解得,m≥$\frac{5}{4}$或m≤$\frac{5}{6}$(不合题意,舍去);
又$\overrightarrow{AC}$在$\overrightarrow{AN}$与$\overrightarrow{AM}$的夹角之内,所以x≥0,y≥0,对应方程有正根;
又m≥$\frac{5}{4}$,∴y1+y2=$\frac{18m}{25}$>0,满足题意,
∴x+y的最小值$\frac{5}{4}$.
【解二】由题意建立平面直角坐标系,如图所示;
设点M(3,a),N(b,4),且0<a<4,0<b<3;
∵$\overrightarrow{AC}$=(3,4),$\overrightarrow{AM}$=(3,a),$\overrightarrow{AN}$=(b,4);
又∵$\overrightarrow{AC}$=x$\overrightarrow{AM}$+y$\overrightarrow{AN}$,(x+y≥1)
∴(3,4)=x(3,a)+y(b,4),
即$\left\{\begin{array}{l}{3x+yb=3}\\{xa+4y=4}\end{array}\right.$,
解得x=$\frac{4b-12}{ab-12}$,y=$\frac{3a-12}{ab-12}$;
最好运用三角换元来做比较好,根据方程组求出x,y(而不是a,b),然后令4-a 分之一为sina,3-b 分之一为cosa,带进去计算出x+y是一个关于sina,cosa的函数,比较容易看出他的最小值
故答案为:$\frac{5}{4}$.
点评 本题考查了平面向量的应用问题,也考查了数形结合的思想与转化思想的应用问题,是较难的题目.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
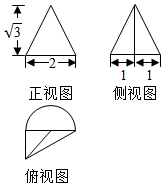
| A. | 4+$\frac{3π}{2}$ | B. | 4+3π | C. | 4+π | D. | 4+$\sqrt{3}$+$\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | B. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{5}{6}$$\overrightarrow{BD}$ | C. | -$\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | D. | $\frac{5}{6}$$\overrightarrow{AC}$-$\frac{1}{6}$$\overrightarrow{BD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=4,p=0.6 | B. | n=6,p=0.4 | C. | n=8,p=0.3 | D. | n=24,p=0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com