
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
分析 由表知道,五项工作后获得的效益值总和最大为17+23+14+11+15=80,但不能同时取得,再分类讨论,得出乙若不承担第二项工作,承担第一项,甲承担第二项工作,则戊承担第四项工作,即可得出结论.
解答 解:由表知道,五项工作后获得的效益值总和最大为17+23+14+11+15=80,但不能同时取得.
要使总和最大,甲可以承担第一或四项工作,丙只能承担第三项工作,丁则不可以承担第三项工作,
所以丁承担第五项工作;乙若承担第四项工作;戊承担第一项工作,此时效益值总和为17+23+14+11+13=78;
乙若不承担第二项工作,承担第一项,甲承担第二项工作,则戊承担第四项工作,
此时效益值总和为17+22+14+11+15=79,所以乙不承担第二项工作,
故答案为:②⑤.
点评 本题考查进行简单的合情推理,考查学生分析解决问题的能力,属于中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丙 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
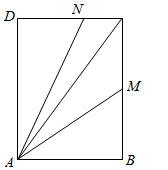 如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.
如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足$\frac{1}{{C{M^2}}}+\frac{1}{{C{N^2}}}=1$,若$\overrightarrow{AC}=x\overrightarrow{AM}+y\overrightarrow{AN}$,则x+y的最小值为$\frac{5}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
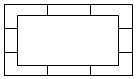 某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)
某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com