
分析 (1)运用等比数列的定义,即可得到$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{b}{a}$,进而得到证明;
(2)①若数列{an}是等差数列,运用等差数列的通项公式,代入即可得到λ=(b-a)2;②若λ=(b-a)2,归纳,猜想an=(n-1)b-(n-2)a=n(b-a)+2a-b,再由数学归纳法证明即可;
(3)求得bn=(1+a)•($\frac{1+b}{1+a}$)n-1,再由恒成立思想,可得(b2-1)2-(b1-1)(b3-1)=(b3-1)2-(b2-1)(b4-1),化简整理可得a=b,进而得到(-1)nanbn=(-1)n•a(1+a),即可得到所求和.
解答 证明:(1)若λ=0,则an2=an-1an+1,n≥2,n∈N,
即有$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{{a}_{n-1}}{{a}_{n-2}}$=…=$\frac{{a}_{3}}{{a}_{2}}$=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{b}{a}$,
则数列{an}是首项为a,公比为$\frac{b}{a}$的等比数列;
(2)①若数列{an}是等差数列,可得公差为b-a,首项为a,
即有an=a+(n-1)(b-a),
则λ=an2-an-1an+1=[a+(n-1)(b-a)]2-[a+(n-2)(b-a)][a+n(b-a)]
=2a(n-1)(b-a)+(n-1)2(b-a)2-n(n-2)(b-a)2-(2n-2)a(b-a)=(b-a)2;
②若λ=(b-a)2,即an2=an-1an+1+(b-a)2,(n≥2,n∈N),
由a1=a,a2=b,可得a22=a1a3+(b-a)2,解得a3=2b-a,
同样可得a4=3b-2a,…,猜想an=(n-1)b-(n-2)a=n(b-a)+2a-b,
证明:当n=1时,a1=b-a+2a-b=a,成立;
当n=2时,a2=2b-2a+2a-b=b,成立;
假设n≤k(k≥2,k∈N)有ak=k(b-a)+2a-b,
且ak2=ak-1ak+1+(b-a)2,
可得ak+1=$\frac{{{a}_{k}}^{2}-(b-a)^{2}}{{a}_{k-1}}$=$\frac{[k(b-a)+2a-b]^{2}-(b-a)^{2}}{(k-1)(b-a)+2a-b}$=$\frac{[k(b-a)+a](kb-ka+3a-2b)}{kb-ka+3a-2b}$=(k+1)(b-a)+2a-b;
故当n=k+1时,ak+1=(k+1)(b-a)+2a-b,成立.
综上可得,数列{an}是等差数列的充要条件是λ=(b-a)2;
(3)对任意的n∈N*,满足bn-an=1,可得b1=1+a,b2=1+b,
公比为$\frac{1+b}{1+a}$,bn=(1+a)•($\frac{1+b}{1+a}$)n-1,
an=bn-1=(1+a)•($\frac{1+b}{1+a}$)n-1-1,
即有(bn-1)2=(bn-1-1)(bn+1-1)+λ,
则(b2-1)2=(b1-1)(b3-1)+λ,
(b3-1)2=(b2-1)(b4-1)+λ,
可得b2-a($\frac{(1+b)^{2}}{1+a}$-1)=($\frac{(1+b)^{2}}{1+a}$-1)2-b($\frac{(1+b)^{3}}{(1+a)^{2}}$-1),
化简整理可得a=b,
则(-1)nanbn=(-1)n•a(1+a),
则数列{(-1)nanbn}的前2n项和
-a(1+a)+a(1+a)-a(1+a)+a(1+a)-…+a(1+a)=0即为常数.
点评 本题考查等差数列和等比数列的定义和通项公式的运用,考查充要条件的证明和数列的求和,注意运用数学归纳法,考查化简整理的运算能力,属于难题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $A_5^5A_5^5$ | B. | $A_4^4A_6^6$ | C. | $A_4^4A_5^5$ | D. | $A_5^5A_6^4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
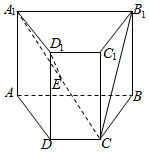 已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E为A1C的中点
已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E为A1C的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 没服用药 | 22 | y | 60 |
| 服用药 | x | 50 | 60 |
| 总计 | 32 | t | 120 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com