
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
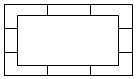 某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)
某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(1,-2) | B. | $\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(6,4) | C. | $\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(5,7) | D. | $\overrightarrow{a}$=(-3,-1),$\overrightarrow{b}$=(3,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com