
分析 (Ⅰ)求得f(x)的导数,求得切线的斜率和切点,运用点斜式方程可得切线的方程,代入A的坐标,解方程可得m的值;
(Ⅱ)求出f′(x)=$\frac{2}{x}$-mx-(1-2m)=$\frac{(x-2)(-mx-1)}{x}$,x>0,讨论:当m≥0时,当$-\frac{1}{2}<m<0$,求得单调区间和极值,讨论极值符号,即可得到所求零点个数.
解答 解:(Ⅰ)f(x)定义域为(0,+∞)
导数f′(x)=$\frac{2}{x}$-mx-(1-2m),
可得切线的斜率为f′(1)=m+1,且$f(1)=\frac{3m}{2}-1$,
所求切线方程 $y-(\frac{3m}{2}-1)=(m+1)({x-1})$,
将点(2,-1)代入切线方程,可得-$\frac{3}{2}$m=1+m,
得 $m=-\frac{2}{5}$;
(Ⅱ)由(Ⅰ)可知f′(x)=$\frac{2}{x}$-mx-(1-2m)=$\frac{(x-2)(-mx-1)}{x}$,x>0,
当m≥0时,-mx-1<0恒成立,
所以x>2时,f′(x)<0,f(x)在(2,+∞)是增函数;
当0<x<2时,f′(x)>0,f(x)在(0,2)是减函数,
f(x)极小值f(2)=2ln2+2m-2;
当f(2)>0,即m>1-ln2时,f(x)有两个零点;
当f(2)=0,即m=1-ln2时,f(x)有一个零点;
当f(2)<0,0≤m<1-ln2时,f(x)无零点;
当m<0,f′(x)=0,得x1=2,${x_2}=-\frac{1}{m}$
当$-\frac{1}{2}<m<0$,f(x)分别在$(-\frac{1}{m},+∞)$,(0,2)是增函数,
f(x)在$(2,-\frac{1}{m})$是减函数,
f(x)极小值f(2)=2ln2+2m-2<0,f(x)至多一个零点.
又y=2lnx是增函数,$y=-\frac{1}{2}m{x^2}-(1-2m)x$是开口向上的抛物线,
所以f(x)必有正值,即f(x)在$-\frac{1}{2}<m<0$有唯一零点;
综上,m>1-ln2时,f(x)有两个零点;
m=1-ln2或$-\frac{1}{2}<m<0$时,f(x)有一个零点;
0≤m<1-ln2,f(x)没有零点.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,考查函数方程的转化思想,函数零点的个数,注意运用分类讨论的思想方法,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
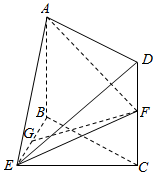 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com