
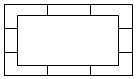
 某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)
某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)分析 (1)设展示框外框的长为xcm,宽为ycm,则内框长为(x-16)cm,宽为(y-8)cm,利用x,y表示面积,列出面积表达式,变形,利用基本不等式求其最小值;
(2)利用(1)得到木条的长度表达式,变形,结合基本不等式求最小值.
解答 解:(1)设展示框外框的长为xcm,宽为ycm,则内框长为(x-16)cm,宽为(y-8)cm,由题意x>16,y>8,因为内框的面积为3200cm2,所以(x-16)(y-8)=3200,所以$y=\frac{3200}{x-16}+8$,外框面积为S=xy=8x+$\frac{3200x}{x-16}$=3328+8(x-16)+$\frac{3200×16}{x-16}$,因为x>16,所以x-16>0,所以S≥3328+2$\sqrt{8(x-16)×\frac{3200×16}{x-16}}$=3328+1280=4608,当且仅当8(x-16)=$\frac{16×3200}{x-16}$即x=96时等号成立,
所以外框的长与宽分别是96cm,48cm时,才能使外框矩形面积最小;
(2)由(1)可知,所用木条的总长度为4(x+y)=4(x+8+$\frac{3200}{x-16}$)=4(x-16+$\frac{3200}{x-16}$+24)≥4(2$\sqrt{3200}$+24)=96+320$\sqrt{2}$,当且仅当x-16=$\frac{3200}{x-16}$即x=16+40$\sqrt{2}$,y=8+40$\sqrt{2}$时等号成立;
所以外框的长与宽分别是(16+40$\sqrt{2}$)cm,(8+40$\sqrt{2}$)cm时,才能使制作整个展示框所用木条最少
点评 本题考查了基本不等式在实践中的应用;关键是由题意列出面积和长度的不等式,凑出基本不等式的形式,利用基本不等式求最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
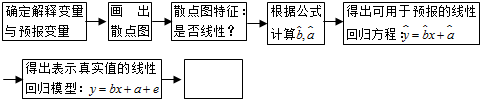
| A. | 预报 | B. | 计算真实值y | C. | 比较模型效果 | D. | 残差异常分析 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com