
分析 根据f(x)存在反函数f-1(x),得出f(x)是定义域上的单调函数,求出a的值以及f(x)的解析式,即可求出f(1)+f-1(-4)的值.
解答 解:∵函数f(x)=(x-a)|x|=$\left\{\begin{array}{l}{{x}^{2}-ax,x≥0}\\{{-x}^{2}+ax,x<0}\end{array}\right.$,
且f(x)存在反函数f-1(x),
∴f(x)是定义域R的单调增函数,
∴a=0,
∴f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{{-x}^{2},x<0}\end{array}\right.$,
∴f(1)+f-1(-4)=1+(-2)=-1.
故答案为:-1
点评 本题考查了反函数的定义与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丙 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
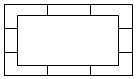 某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)
某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2.(不计木料的粗细与接头处损耗)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com