
【题目】对于任意![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“
,则称这个数列为“![]() 数列”.
数列”.
(1)已知数列:![]() ,
,![]() ,
,![]() 是“
是“![]() 数列”,求实数
数列”,求实数![]() 的取值范围;
的取值范围;
(2)已知等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,数列
,数列![]() 是“
是“![]() 数列”,求首项
数列”,求首项![]() 的取值范围;
的取值范围;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() ,
,![]() . 设
. 设![]() ,是否存在实数
,是否存在实数![]() ,使得数列
,使得数列![]() 为“
为“![]() 数列”. 若存在,求实数
数列”. 若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】要想得到函数y=sin2x+1的图象,只需将函数y=cos2x的图象( )
A.向左平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
B.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
C.向左平移 ![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
D.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选做题:几何证明选讲 如图,ABCD是边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点F,延长CF交AB于E.
(1)求证:E是AB的中点;
(2)求线段BF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(1)求证:MN∥平面BDE;
(2)求二面角CEMN的正弦值;
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.得到甲、乙两位学生成绩的茎叶图.
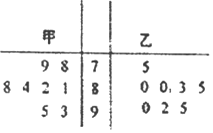
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(m) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则
,则![]() _____.
_____.
【答案】![]()
【解析】
分子分母同时除以![]() ,把目标式转为
,把目标式转为![]() 的表达式,代入可求.
的表达式,代入可求.
![]() ,则
,则![]()
![]()
故答案为:![]() .
.
【点睛】
本题考查三角函数的化简求值,常用方法:(1)弦切互化法:主要利用公式![]() , 形如
, 形如![]() 等类型可进行弦化切;(2)“1”的灵活代换
等类型可进行弦化切;(2)“1”的灵活代换![]() 和
和![]() 的关系进行变形、转化.
的关系进行变形、转化.
【题型】填空题
【结束】
15
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 中点,连接
中点,连接![]() ,则异面直线
,则异面直线![]() 和
和![]() 所成角的余弦值为_____.
所成角的余弦值为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学旅游局欲将一块长20百米,宽10百米的矩形空地ABCD建成三星级乡村旅游园区,园区内有一景观湖EFG(如图中阴影部分)以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy,O为园区正门,园区北门P在y正半轴上,且PO=10百米。景观湖的边界线符合函数![]() 的模型。
的模型。
(1)若建设一条与AB平行的水平通道,将园区分成面积相等的两部分,其中湖上的部分建成玻璃栈道,求玻璃栈道的长度。
(2)若在景观湖边界线上一点M修建游船码头,使得码头M到正门O的距离最短,求此时M点的横坐标。
(3)设图中点B为仓库所在地,现欲在线段OB上确定一点Q建货物转运站,将货物从点B经Q点直线转运至点P(线路PQ不穿过景观湖),使货物转运距离QB+PQ最短,试确定点P的位置。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com