
已知 ,函数
,函数 ,当
,当 时,
时,  的值域是
的值域是 .
.
(1)求常数 的值;
的值;
(2)当 时,设
时,设 ,求
,求 的单调区间.
的单调区间.
(1) (2)
(2)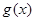 的单调递增区间为
的单调递增区间为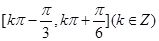 ,单调递减区间为
,单调递减区间为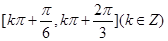
解析试题分析:(1)先由辅助角公式化为一个角的三角函数,按照复合函数求值域的方法,结合所给 的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域,注意分类讨论.(2)先利用诱导公式求出
的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域,注意分类讨论.(2)先利用诱导公式求出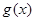 的解析式,利用复合函数单调区间的求法求出
的解析式,利用复合函数单调区间的求法求出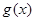 的单调区间.
的单调区间.
试题解析:(1)由题设知: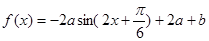 1分
1分
由 知:
知: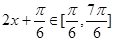 ,得
,得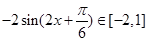 3分
3分
∴当 时,
时, 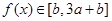 , 即
, 即 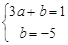 ,
, 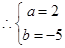 ; 5分
; 5分
当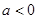 时,
时, 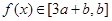 , 即
, 即 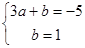
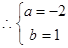 7分
7分
所以 8分
8分
(2)由(1)及题设知: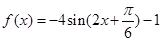 9分
9分
∴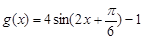 10分
10分
由 得
得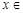
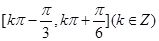
由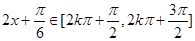 得
得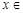
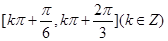 12分
12分
∴ 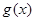 的单调递增区间为
的单调递增区间为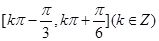
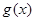 的单调递减区间为
的单调递减区间为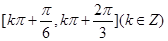 14分
14分
(其他写法参照给分)
考点:三角变换;三角函数在某个区间上的值域;诱导公式;三角函数单调性


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,A,B是单位圆上的两个质点,点B坐标为(1,0),∠BOA=60°.质点A以1 rad/s的角速度按逆时针方向在单位圆上运动,质点B以1 rad/s的角速度按顺时针方向在单位圆上运动.
(1)求经过1 s 后,∠BOA的弧度;
(2)求质点A,B在单位圆上第一次相遇所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com