
已知函数 .
.
(1)把 的解析式
的解析式 Acos(
Acos( )+B的形式,并用五点法作出
)+B的形式,并用五点法作出 在一个周期上的简图;(要求列表)
在一个周期上的简图;(要求列表)
(2)说出 的图像经过怎样的变换
的图像经过怎样的变换 的图像.
的图像.
(1)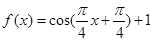 ;(2)
;(2) 的图像向左平移
的图像向左平移 个单位得到
个单位得到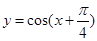 图像的;纵坐标不变,横坐标变为原来的
图像的;纵坐标不变,横坐标变为原来的 倍得到
倍得到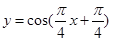 的图像;向上平移1个单位得到
的图像;向上平移1个单位得到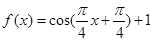 的图像.
的图像.
解析试题分析:解题思路:(1)利用二倍角的变形“降次升角”变形即得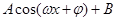 的形式,再利用“列表、描点、连线”法进行作简图;(2)利用“平移、伸缩、平移”步骤进行图像变换.规律总结:三角函数的化简,即利用同角三角函数基本关系式、诱导公式、两角和差的三角公式、二倍角公式及其变形化成
的形式,再利用“列表、描点、连线”法进行作简图;(2)利用“平移、伸缩、平移”步骤进行图像变换.规律总结:三角函数的化简,即利用同角三角函数基本关系式、诱导公式、两角和差的三角公式、二倍角公式及其变形化成 的形式;三角函数的图像变换一般两个途径:①先左右平移(左加右减),再沿横坐标轴进行伸缩(
的形式;三角函数的图像变换一般两个途径:①先左右平移(左加右减),再沿横坐标轴进行伸缩( 缩短,
缩短, 伸长),再沿纵坐标轴进行伸缩(
伸长),再沿纵坐标轴进行伸缩( 缩短,
缩短,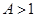 伸长).最后上下平移(上加下减);②先沿横坐标轴进行伸缩(
伸长).最后上下平移(上加下减);②先沿横坐标轴进行伸缩( 缩短,
缩短, 伸长),再左右平移(左加右减),再沿纵坐标轴进行伸缩(
伸长),再左右平移(左加右减),再沿纵坐标轴进行伸缩( 缩短,
缩短,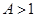 伸长).最后上下平移(上加下减).
伸长).最后上下平移(上加下减).
注意点:先伸缩后平移时,要注意平移的单位 的图像由
的图像由 向左或右平移
向左或右平移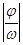 个单位.
个单位.
试题解析:(1)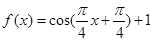 .
.
列表如下:
0 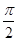
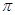
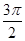

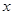
-1 1 3 5 7 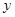
2 1 0 1 2 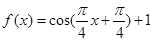 的简图如下:
的简图如下:
(2) 的图像向左平移
的图像向左平移 个单位得到
个单位得到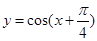 图像的;纵坐标不变,横坐标变为原来的
图像的;纵坐标不变,横坐标变为原来的 倍得到
倍得到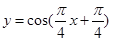 的图像;向上平移1个单位得到
的图像;向上平移1个单位得到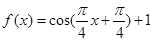 的图像.
的图像.
考点:三角恒等变换、三角函数的图像变换.


科目:高中数学 来源: 题型:解答题
已知函数
(1)求函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若将函数的图像向右平移 个单位,得到函数
个单位,得到函数 的图像,求
的图像,求 在区间
在区间 上的最大值和最小值,并求出相应的x的取值。
上的最大值和最小值,并求出相应的x的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com