
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 由题意得f(x)的对称轴为$x=\frac{π}{4}$,及f(x)=$\sqrt{1+{a}^{2}}$sin(x+α),由此得到f(x)的最值的关系式,得到a=1,由此得到f(x)的最大值.
解答 选B.解:由题意得f(x)的对称轴为$x=\frac{π}{4}$,
f(x)=asinx+cosx=$\sqrt{1+{a}^{2}}$sin(x+α)
当$x=\frac{π}{4}$时,f(x)取得最值$\sqrt{{a^2}+1}$
即$\frac{{\sqrt{2}}}{2}({a+1})=\sqrt{{a^2}+1}$,得a=1,
∴f(x)的最大值为$\sqrt{2}$.
故选B.
点评 本题考查正弦函数图象和性质,是基础题,解题时要认真审题,仔细解答,注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
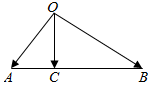 如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )
如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com