
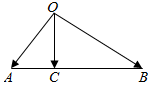
 如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )
如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
分析 根据条件便可得出△AOB为Rt△,且∠AOB=90°,从而在Rt△AOB中,可求出∠OAB=60°,进而便得到$\overrightarrow{OC}⊥\overrightarrow{AB}$,从而$\overrightarrow{OC}•\overrightarrow{AB}=0$,带入$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB},\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$进行数量积的运算便可得到3n-m=0.而由条件容易得出m+n=1,这两式联立即可解出m,n,从而便可求出m-n的值.
解答 解:∵$\overrightarrow{OA}•\overrightarrow{OB}=0$;
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$;
∴∠AOB=90°,且$|\overrightarrow{OA}|=1,|\overrightarrow{OB}|=\sqrt{3}$;
∴$|\overrightarrow{AB}|=2$;
∴$cos∠OAB=\frac{\sqrt{3}}{2}$;
∴∠OAB=60°;
又∠AOC=30°;
∴∠OCA=90°;
即$\overrightarrow{OC}⊥\overrightarrow{AB}$;
∴$\overrightarrow{OC}•\overrightarrow{AB}=\overrightarrow{OC}•(\overrightarrow{OB}-\overrightarrow{OA})$
=$(m\overrightarrow{OA}+n\overrightarrow{OB})•(\overrightarrow{OB}-\overrightarrow{OA})$
=$m\overrightarrow{OA}•\overrightarrow{OB}-m{\overrightarrow{OA}}^{2}+n{\overrightarrow{OB}}^{2}-n\overrightarrow{OA}•\overrightarrow{OB}$
=0-m+3n-0
=0;
即3n-m=0①;
∵$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,且A,C,B三点共线;
∴m+n=1②;
∴①②联立得,$m=\frac{3}{4},n=\frac{1}{4}$;
∴$m-n=\frac{1}{2}$.
故选:B.
点评 考查向量垂直的充要条件,三角函数的定义,已知三角函数值求角,向量减法的几何意义,以及向量数量积的运算及计算公式,三点A,B,C共线的充要条件.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:
某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分且必要条件 | |
| B. | 充分不必要条件 | |
| C. | 必要不充分条件 | |
| D. | 既不是的充分条件也不是的必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com