
分析 先确定定义域,再求导,由导函数的正负得到原函数的单调性,由单调性得到最大最小值,从而得到值域.
解答 解:∵y=$\sqrt{1+x}$+2$\sqrt{1-x}$,
∴函数的定义域为:[-1,1],
y′=$\frac{1}{2\sqrt{1+x}}$-$\frac{1}{\sqrt{1-x}}$=$\frac{\sqrt{1-x}-2\sqrt{1+x}}{2\sqrt{1-{x}^{2}}}$,
令y′=0,
得x=-$\frac{3}{5}$,
∴y在[-1,-$\frac{3}{5}$)是单调递增的,在(-$\frac{3}{5}$,1]是单调递减的.
∴y的最大值在x=-$\frac{3}{5}$处取得,为$\sqrt{10}$
y有最小值为$\sqrt{2}$,在x=1处取得,
∴函数y=$\sqrt{1+x}$+2$\sqrt{1-x}$的值域为[$\sqrt{2}$,$\sqrt{10}$].
点评 本题考查确定定义域以及由导函数确定单调性,从单调性里面找到最大最小值.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
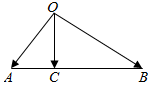 如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )
如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{4π-3\sqrt{2}}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{2π-1}{2π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com