
 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:
某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:分析 (1)用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,得出众数,
利用中位数的两边频率相等,求出中位数;
(2)利用各小组底边的中点值乘以对应频率,再求和,得出数据的平均值.
解答 解:(1)用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,得众数为65,
又∵第一个小矩形的面积为0.3,
∴设第二个小矩形底边的一部分长为x,
则x×0.04=0.2,得x=5,
∴中位数为60+5=65;
(2)依题意,平均成绩为:
55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,
∴平均成绩约为67.
点评 本题考查了利用频率分布直方图求众数与中位数、平均数的应用问题,是基础题目.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,2} | C. | {x|0≤x≤$\sqrt{3}$} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(sinB) | C. | f(cosA)<f(cosB) | D. | f(cosA)>f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
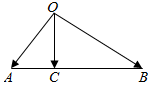 如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )
如图所示,已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点C在线段AB上,且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m-n等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com