
分析 (1)设正项等差数列{an}的公差为d,由于2Sn=an•an+1,可得:当n=1时,2a1=a1•a2,解得a2=2.当n≥2时,可得2an=an(an+1-an-1),即an+1-an-1=2.可得d,再利用通项公式即可得出.
(2)由(1)可得:Sn=$\frac{n(n+1)}{2}$.可得bn=$\frac{{S}_{n}-1}{{2}^{{a}_{n}}}$=$\frac{n(n+1)}{{2}^{n+1}}$-$\frac{1}{{2}^{n}}$,令An为数列$\{\frac{n(n+1)}{{2}^{n+1}}\}$的前n项和,两次利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 (1)解:设正项等差数列{an}的公差为d,
∵2Sn=an•an+1,∴当n=1时,2a1=a1•a2,解得a2=2.
当n≥2时,2Sn-1=an-1•an,∴2an=an(an+1-an-1),
∵an>0,∴an+1-an-1=2.
∴(an+1-an)+(an-an-1)=2d=2,解得d=1.
∴an=a2+(n-2)d=2+(n-2)=n.
(2)证明:由(1)可得:Sn=$\frac{n(n+1)}{2}$.
∴bn=$\frac{{S}_{n}-1}{{2}^{{a}_{n}}}$=$\frac{\frac{n(n+1)}{2}-1}{{2}^{n}}$=$\frac{n(n+1)}{{2}^{n+1}}$-$\frac{1}{{2}^{n}}$,
令An为数列$\{\frac{n(n+1)}{{2}^{n+1}}\}$的前n项和,
则An=$\frac{1×2}{{2}^{2}}+\frac{2×3}{{2}^{3}}$+…+$\frac{n(n+1)}{{2}^{n+1}}$,
$\frac{1}{2}{A}_{n}$=$\frac{1×2}{{2}^{3}}+\frac{2×3}{{2}^{4}}$+…+$\frac{(n-1)n}{{2}^{n+1}}$+$\frac{n(n+1)}{{2}^{n+2}}$,
∴$\frac{1}{2}{A}_{n}$=$\frac{2}{{2}^{2}}+2(\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n}{{2}^{n+1}})$-$\frac{n(n+1)}{{2}^{n+2}}$,
令Bn=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+$…+$\frac{n}{{2}^{n+1}}$,
$\frac{1}{2}{B}_{n}$=$\frac{1}{{2}^{3}}+\frac{2}{{3}^{4}}$+…+$\frac{n-1}{{2}^{n+1}}$+$\frac{n}{{2}^{n+2}}$,
∴$\frac{1}{2}{B}_{n}$=$\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n+1}}$-$\frac{n}{{2}^{n+2}}$=$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+2}}$=$\frac{1}{2}-\frac{2+n}{{2}^{n+2}}$,
∴Bn=1-$\frac{2+n}{{2}^{n+1}}$.
∴$\frac{1}{2}{A}_{n}$=$\frac{1}{2}$+2$(1-\frac{2+n}{{2}^{n+1}}-\frac{1}{4})$-$\frac{n(n+1)}{{2}^{n+2}}$=2-$\frac{{n}^{2}+5n+8}{{2}^{n+2}}$,
∴An=4-$\frac{{n}^{2}+5n+8}{{2}^{n+1}}$.
∴Tn=b1+b2+…+bn=4-$\frac{{n}^{2}+5n+8}{{2}^{n+1}}$-$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=3-$\frac{{n}^{2}+5n+8}{{2}^{n+1}}$+$\frac{1}{{2}^{n}}$=3-$\frac{{n}^{2}+5n+6}{{2}^{n+1}}$<3.
∴Tn<3.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Asin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示,若$\overrightarrow{PQ}$•$\overrightarrow{QS}$=$\frac{{π}^{2}}{8}$-8,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示,若$\overrightarrow{PQ}$•$\overrightarrow{QS}$=$\frac{{π}^{2}}{8}$-8,则函数f(x)的解析式为( )| A. | f(x)=2sin(3x-$\frac{π}{4}$) | B. | f(x)=2sin(3x+$\frac{π}{4}$) | C. | f(x)=2sin(2x+$\frac{π}{3}$) | D. | f(x)=2sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
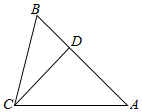 △ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.
△ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只取正号 | B. | 只取负号 | ||
| C. | 可取正号,也可取负号 | D. | 可取正号,负号,也可取零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com