Question

14．在平面直角坐标系中，O是坐标原点，两定点A，B满足$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=\overrightarrow{OA}•\overrightarrow{OB}=2$，则$\overrightarrow{OA}，\;\overrightarrow{OB}$的夹角为60°；点集$\{\left.{P\;}\right|\;\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;，\;λ+μ≤1\;，\;λ≥0\;，\;μ≥0\}$所表示的区域的面积是$\sqrt{3}$．

Answer 1

分析 由两定点A，B满足$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=\overrightarrow{OA}•\overrightarrow{OB}=2$，运用数量积的定义，说明O，A，B三点构成边长为2的等边三角形，设出两个定点的坐标，再设出P点坐标，由平面向量基本定理，把P的坐标用A，B的坐标及λ，μ表示，把不等式0≤λ+μ≤1去绝对值后可得线性约束条件，画出可行域可求点集P所表示区域的面积．

解答 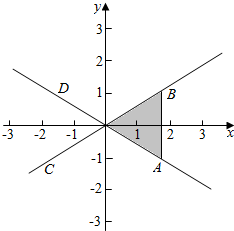解：由两定点A，B满足$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=\overrightarrow{OA}•\overrightarrow{OB}=2$，
说明O，A，B三点构成边长为2的等边三角形．
不妨O，A，B三点构成边长为2的等边三角形．
设A（$\sqrt{3}$，-1），B（$\sqrt{3}$，1）．再设P（x，y）．
由$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，得：（x，y）=（$\sqrt{3}$λ，-λ）+（$\sqrt{3}$μ，μ）
=（$\sqrt{3}$（λ+μ），μ-λ）．
所以$\left\{\begin{array}{l}{λ+μ=\frac{\sqrt{3}}{3}x}\\{μ-λ=y}\end{array}\right.$，解得$\left\{\begin{array}{l}{λ=\frac{\sqrt{3}}{6}x-\frac{1}{2}y}\\{μ=\frac{\sqrt{3}}{6}x+\frac{1}{2}y}\end{array}\right.$①．
由λ+μ≤1．
所以①等价于$\left\{\begin{array}{l}{\frac{\sqrt{3}}{6}x-\frac{1}{2}y≥0}\\{\frac{\sqrt{3}}{6}x+\frac{1}{2}y≥0}\\{0＜x≤\sqrt{3}}\end{array}\right.$，
可行域如图中等边三角形AOB及其内部区域，
则区域面积为$\frac{\sqrt{3}}{4}$×4=$\sqrt{3}$．
故答案为：60⁰，$\sqrt{3}$．

点评 本题考查了平面向量的基本定理及其意义，考查了二元一次不等式（组）所表示的平面区域，考查了数学转化思想方法，解答此题的关键在于读懂题意，属中档题．