
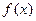 满足下列条件:
满足下列条件: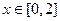 ,总有
,总有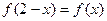 ,且
,且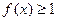 ,
,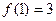 ;
;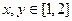 ,若
,若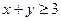 ,则
,则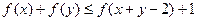 .
.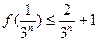 (
(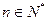 );(2)
);(2)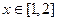 时,
时,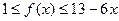 .
.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
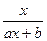 (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
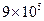 hm
hm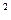 .地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表:
.地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表:| 观测年份 | 该地区沙漠面积比原有面积增加数 hm 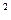 |
| 1998 | 2000 |
| 1999 | 4000 |
| 2000 | 6001 |
| 2001 | 7999 |
| 2002 | 10001 |
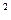 ?
?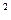 沙漠,但沙漠面积仍按原有速度增加,那么到哪一年年底,这个地区的沙漠面积将小于
沙漠,但沙漠面积仍按原有速度增加,那么到哪一年年底,这个地区的沙漠面积将小于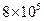 hm
hm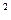 ?
?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com