
(本小题满分12分)
设函数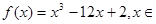 R,求函数
R,求函数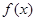 在区间
在区间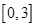 上的最小值.
上的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
设函数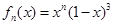 在
在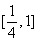 上的最大值为
上的最大值为 (
(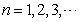 ).
).
(1)求数列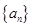 的通项公式;
的通项公式;
(2)求证:对任何正整数n (n≥2),都有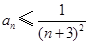 成立;
成立;
(3)设数列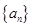 的前n项和为Sn,求证:对任意正整数n,都有
的前n项和为Sn,求证:对任意正整数n,都有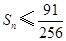 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x3+ax2+bx.
(1)若函数y=f(x)在x=2处有极值-6,求y=f(x)的单调递减区间;
(2)若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=ln x-p(x-1),p∈R.
(1)当p=1时,求函数f(x)的单调区间;
(2)设函数g(x)=xf(x)+p(2x2-x-1)(x≥1),求证:当p≤- 时,有g(x)≤0.
时,有g(x)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.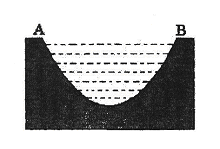
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com