
���� ����ȷ����Բ�ļ���������������ԲC�ķ��̣�
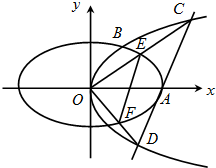
������P��x1��y1����Q��x2��y2����ֱ��l��y=k��x-1������ԲC������ȷ��M�����꣬��һ���ɵ�MN�е����꣬����M��N����ֱ��l�Գƣ�����M��N����ֱ����ֱ��l��ֱ��������k��ֵ��
��� �⣺����������y2=8x��
���Խ�������Ϊ��2��0������A��2��0����
����a=2��
����Ϊe=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$������c=$\sqrt{3}$��
����b=1��
������ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$�� ����4�֣�
������P��x1��y1����Q��x2��y2����
��Ϊ$\overrightarrow{AM}=\overrightarrow{AP}+\overrightarrow{AQ}$��
����$\overrightarrow{AM}$=��x1+x2-4��y1+y2����
����M��x1+x2-2��y1+y2����
��ֱ��l��y=k��x-1������ԲC�������ã�4k2+1��x2-8k2x+4k2-4=0��
��x1+x2-2=-$\frac{2}{4{k}^{2}+1}$��y1+y2=$\frac{-2k}{4{k}^{2}+1}$��
��M��-$\frac{2}{4{k}^{2}+1}$��$\frac{-2k}{4{k}^{2}+1}$����
��N��0��y3������MN�е�����Ϊ��-$\frac{1}{4{k}^{2}+1}$��$\frac{-k}{4{k}^{2}+1}+\frac{{y}_{3}}{2}$����
��ΪM��N����ֱ��l�Գƣ�
����MN���е���ֱ��l�ϣ�
����$\frac{-k}{4{k}^{2}+1}+\frac{{y}_{3}}{2}$=k��-$\frac{1}{4{k}^{2}+1}$-1�������y3=-2k����N��0��-2k����
����M��N����ֱ��l�Գƣ�����M��N����ֱ����ֱ��l��ֱ��
����$\frac{\frac{-2k}{4{k}^{2}+1}-��-2k��}{\frac{-2}{4{k}^{2}+1}-0}•k=-1$�����k=��$\frac{\sqrt{2}}{2}$�� ����14�֣�
���� ���⿼�������ߵļ������ʣ�������Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{-a{\;}^{2}-c{\;}^{2}}{c{\;}^{2}}$ | B�� | $\frac{c����-1��}{a}$ | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {-1} | C�� | {$\frac{1}{2}$} | D�� | {-1��2} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com