
���� ��1��������Բ�ı����̼�����Բ�ĵڶ����弴�ɵó���
��2����DE��x��ʱ����x=1������Բ���̽��D$��1��\frac{3}{2}��$��E$��1��-\frac{3}{2}��$���ɵ�ֱ��AD�ķ��̣�y=$\frac{1}{2}��x+2��$�����M��N���ɵ���MNΪֱ����Բ����F��1��0����G��7��0����
����֤����MNΪֱ����Բ������������㣮��ֱ��DE�ķ���Ϊ��my=x-1��D��x1��y1����E��x2��y2��������Բ����������Ϊ��3m2+4��y2+6my-9=0��ֱ��AD�ķ���Ϊ��y=$\frac{{y}_{1}}{m{y}_{1}+3}��x+2��$���ɵ�M$��4��\frac{6{y}_{1}}{m{y}_{1}+3}��$��ͬ���ɵ�N$��4��\frac{6{y}_{2}}{m{y}_{2}+3}��$�����ø���ϵ���Ĺ�ϵ��֤��$\overrightarrow{FM}•\overrightarrow{FN}$=0�����ɵó����ۣ�
��� �⣺��1������ԲC��$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1���ɵ�a=2��c=1���ҽ���F��1��0������������e=$\frac{1}{2}$��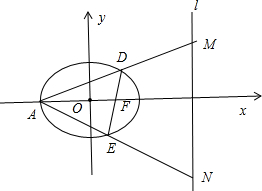
����ԲC������һ��P����F�ľ������P��ֱ��l��x=m�ľ���֮��Ϊ$\frac{1}{2}$��
��$m=\frac{{a}^{2}}{c}$=4��
��ֱ��l����Ϊ��x=4��
��2����DE��x��ʱ����x=1������Բ���̽��y=$��\frac{3}{2}$����D$��1��\frac{3}{2}��$��E$��1��-\frac{3}{2}��$��
�ɵ�ֱ��AD�ķ��̣�y=$\frac{1}{2}��x+2��$�����M��4��3����ͬ���ɵ�N��4��-3����
�ɵ���MNΪֱ����Բ����F��1��0����G��7��0����
����֤����MNΪֱ����Բ������������㣮
֤������ֱ��DE�ķ���Ϊ��my=x-1��D��x1��y1����E��x2��y2����
����$\left\{\begin{array}{l}{my=x-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$������3m2+4��y2+6my-9=0��
��y1+y2=-$\frac{6m}{3{m}^{2}+4}$��y1y2=$\frac{-9}{3{m}^{2}+4}$��
ֱ��AD�ķ���Ϊ��y=$\frac{{y}_{1}}{m{y}_{1}+3}��x+2��$���ɵ�M$��4��\frac{6{y}_{1}}{m{y}_{1}+3}��$��
ͬ���ɵ�N$��4��\frac{6{y}_{2}}{m{y}_{2}+3}��$��
��$\overrightarrow{FM}•\overrightarrow{FN}$=$��3��\frac{6{y}_{1}}{m{y}_{1}+3}��$•$��3��\frac{6{y}_{2}}{m{y}_{2}+3}��$=9+$\frac{36{y}_{1}{y}_{2}}{{m}^{2}{y}_{1}{y}_{2}+3m��{y}_{1}+{y}_{2}��+9}$
=9+$\frac{36��\frac{-9}{3{m}^{2}+4}}{\frac{-9{m}^{2}}{3{m}^{2}+4}-\frac{18{m}^{2}}{3{m}^{2}+4}+9}$=9-9=0��
����MNΪֱ����Բ���һ����F��1��0����G��7��0����
ͬ����֤����MNΪֱ����Բ���һ����G��7��0����
�����MNΪֱ����Բ���һ����F��1��0������7��0����
���� ���⿼������Բ�ı����̼������ʡ�Բ�����ʡ�ֱ������Բ�ཻת��Ϊ���������ɵø���ϵ����ϵ��ֱ�ߵķ��̡�������ֱ���������Ĺ�ϵ�����������������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ⳤΪ1��������ABCD-A1B1C1D1�У�M��A1D1���е㣬��P�ڲ���BCC1B1���˶��������������⣺
���ⳤΪ1��������ABCD-A1B1C1D1�У�M��A1D1���е㣬��P�ڲ���BCC1B1���˶��������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
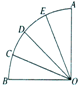 ����AOB�İ뾶Ϊ1��Բ�Ľ�Ϊ90�㣬��C��D��E����AB�ֳ��ĵȷ֣�����OC��OD��OE����ͼ�����е����������ȡ��һ�������ǡ��Ϊ$\frac{��}{8}$�ĸ����ǣ�������
����AOB�İ뾶Ϊ1��Բ�Ľ�Ϊ90�㣬��C��D��E����AB�ֳ��ĵȷ֣�����OC��OD��OE����ͼ�����е����������ȡ��һ�������ǡ��Ϊ$\frac{��}{8}$�ĸ����ǣ�������| A�� | $\frac{3}{10}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 11 | B�� | 9 | C�� | 7 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com