
 如图,已知圆(x-2)2+y2=$\frac{4}{9}$是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的内接△ABC的内切圆,其中A为椭圆C的左顶点,且椭圆C的离心率为$\frac{{\sqrt{15}}}{4}$,则此椭圆的标准方程为$\frac{x^2}{16}+{y^2}=1$.
如图,已知圆(x-2)2+y2=$\frac{4}{9}$是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的内接△ABC的内切圆,其中A为椭圆C的左顶点,且椭圆C的离心率为$\frac{{\sqrt{15}}}{4}$,则此椭圆的标准方程为$\frac{x^2}{16}+{y^2}=1$. 分析 利用椭圆G的离心率为e=$\frac{\sqrt{15}}{4}$,设左顶点A(-a,0),根据圆(x-2)2+y2=$\frac{4}{9}$是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的内接△ABC的内切圆,求出a,b的值,可求椭圆的标准方程;
解答 解:设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A(-a,0),
∵e=$\frac{\sqrt{15}}{4}$=$\frac{c}{a}$,得c=$\frac{\sqrt{15}}{4}$a,
则b2=a2-c2=$\frac{{a}^{2}}{16}$,
即b=$\frac{a}{4}$,
由圆G(x-2)2+y2=$\frac{4}{9}$是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的内接△ABC的内切圆,
过圆心G作GD⊥AB于D,BC交长轴于H,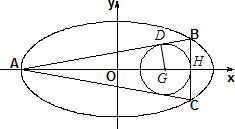
则BH=$\sqrt{\frac{{a}^{2}}{16}-\frac{4}{9}}$,AD=$\sqrt{(a+2)^{2}-(\frac{2}{3})^{2}}$,
∵$\frac{GD}{AD}=\frac{BH}{AH}$,
即$\frac{\frac{2}{3}}{\sqrt{{(a+2)}^{2}-{(\frac{2}{3})}^{2}}}=\frac{\sqrt{\frac{{a}^{2}}{16}-\frac{4}{9}}}{a+2+\frac{2}{3}}$,
解得:a=4,
∴椭圆的标准方程为:$\frac{x^2}{16}+{y^2}=1$
点评 本题考查的知识点是椭圆的简单性质,椭圆的方程,本题计算量比较大,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$] | C. | [2,+∞) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [-$\sqrt{2},0$] | C. | [-$\sqrt{5}$,1] | D. | [1-$\sqrt{5}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{2}$](k∈Z) | B. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) | ||
| C. | [2kπ+π,2kπ+2π](k∈Z) | D. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com