Question

8．若函数f（x）=|x-a|+|x+1|，方程f（x）=$\sqrt{1-{x}^{2}}$有解时，a的取值范围为（　　）

• A． [-2，0]
• B． [-$\sqrt{2}，0$]
• C． [-$\sqrt{5}$，1]
• D． [1-$\sqrt{5}$，0]

Answer 1

分析 方程f（x）=$\sqrt{1-{x}^{2}}$有解可化为函数f（x）=|x-a|+|x+1|与函数y=$\sqrt{1-{x}^{2}}$的图象有交点，利用排除法确定答案即可．

解答 解：若a=1，作函数f（x）=|x-a|+|x+1|与函数y=$\sqrt{1-{x}^{2}}$的图象如下，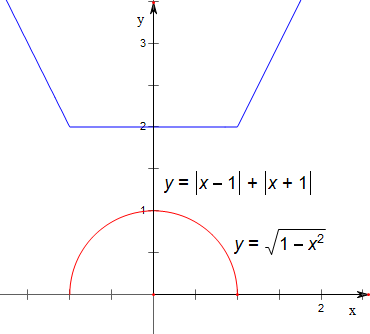

故排除C选项，
若a=-2，作函数f（x）=|x-a|+|x+1|与函数y=$\sqrt{1-{x}^{2}}$的图象如下，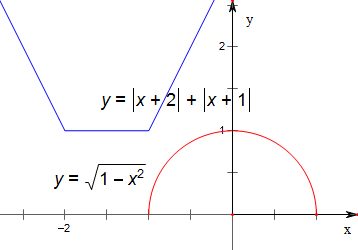

故排除A选项，
若a=-$\sqrt{2}$，作函数f（x）=|x-a|+|x+1|与函数y=$\sqrt{1-{x}^{2}}$的图象如下，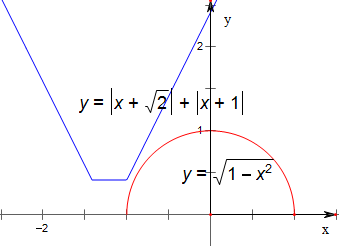

故排除B选项，
故选D．

点评 本题考查了方程的根与函数的图象的交点的关系应用及排除法的应用，属于中档题．