
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]()
【解析】
试题分析:(1)函数f(x)为奇函数,故可得f(x)+f(-x)=0,由此方程求m的值;(2)证明于任意m,f(x)在R上为单调函数,由定义法证明即可,设![]() ∈R,
∈R,![]() ,研究
,研究![]() 的符号,根据单调性的定义判断出结果;(3)因为f(x)在R上为增函数且为奇函数,由此可以将不等式
的符号,根据单调性的定义判断出结果;(3)因为f(x)在R上为增函数且为奇函数,由此可以将不等式![]() 对任意x∈R恒成立,转化为
对任意x∈R恒成立,转化为![]() 即
即![]() 对任意x∈R恒成立,再通过换元进一步转化为二次不等式恒成立的问题即可解出此时的恒成立的条件
对任意x∈R恒成立,再通过换元进一步转化为二次不等式恒成立的问题即可解出此时的恒成立的条件
试题解析:(1)∵![]() ,且
,且![]()
∴![]() (注:通过
(注:通过![]() 求也同样给分)∴
求也同样给分)∴![]()
(2)证明:设![]() ,则
,则![]()
![]()
![]() ∵
∵![]() ∴
∴![]()
∴![]() 即
即![]() 。 所以
。 所以![]() 在R上为增函数。
在R上为增函数。
(3)因为![]() 为奇函数且在R上为增函数,
为奇函数且在R上为增函数,
由![]() 得:
得: ![]()
∴![]() 即
即![]() 对任意
对任意![]() 恒成立。
恒成立。
令![]()
![]() 问题等价于
问题等价于![]() 对任意
对任意![]() 恒成立。
恒成立。
令![]() ,其对称轴
,其对称轴![]()
当![]() 即
即![]() 时,
时,![]() ,符合题意。
,符合题意。
当![]() 时,即
时,即![]() 时,对任意
时,对任意![]() ,
,![]() 恒成立,等价于
恒成立,等价于![]()
解得:![]()
综上所述,当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立
恒成立


科目:高中数学 来源: 题型:
【题目】要产生[-3,3]上的均匀随机数y,现有[0,1]上的均匀随机数x,则y可取为( )
A. -3x B. 3x
C. 6x-3 D. -6x-3
查看答案和解析>>
科目:高中数学 来源: 题型:
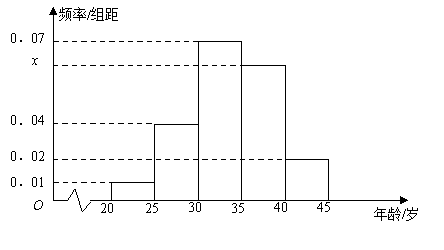
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者. 从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是: ![]() .
.
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人. 记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.

(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且![]() ,求∠BAC.
,求∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 对于任意实数
对于任意实数![]() ,都有
,都有![]() 成立,且
成立,且![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的单调性,并加以证明;
的单调性,并加以证明;
(2)试问:当![]() 时,
时,![]() 是否有最值?如果有,求出最值;如果没有,说明理由;
是否有最值?如果有,求出最值;如果没有,说明理由;
(3)解关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中开展了丰富多彩的社团文化活动,甲,乙,丙三位同学在被问到是否参加过街舞社,动漫社,器乐社这三个社团时,
甲说:我参加过的社团比乙多,但没有参加过动漫社;
乙说:我没有参加过器乐社;
丙说:我们三个人都参加过同一个社团,由此判断乙参加过的社团为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com